题目内容
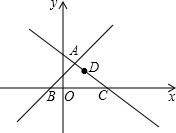 如图,在平面直角坐标系xOy中,直线y=x+1与y=-
如图,在平面直角坐标系xOy中,直线y=x+1与y=-| 3 |
| 4 |
(1)求点A、B、C的坐标;
(2)如△BDC的面积为△ABC面积的两倍,求此时D的坐标;
(3)试写出当BD=CD时,BD的解析式,并求出此时△ABD与△BCD的面积的比值.
考点:两条直线相交或平行问题
专题:
分析:(1)根据两直线解析式,令y=0,求解即可得到B、C点的坐标,两解析式联立求解即可得到点A的坐标;
(2)根据三角形是同底的三角形,如△BDC的面积为△ABC面积的两倍,则△BDC的高为△ABC高的两倍,求D的纵坐标,代入直线y=-
x+3即可求得横坐标,进而求得D的坐标.
(3)设D(m,-
m+3),根据BD=CD列出关于m的方程,解方程求得m的值,进而求得D的坐标,然后根据
=
即可求得△ABD与△BCD的面积的比值.
(2)根据三角形是同底的三角形,如△BDC的面积为△ABC面积的两倍,则△BDC的高为△ABC高的两倍,求D的纵坐标,代入直线y=-
| 3 |
| 4 |
(3)设D(m,-
| 3 |
| 4 |
| S△ABD |
| S△BCD |
| S△ABC-S△BDC |
| S△BCD |
解答:解:(1)
,
解得
.
所以A(
,
),
令y=0,则x+1=0,解得x=-1,
则-
x+3=0,解得x=4,
所以B(-1,0),C(4,0).
(2)∵△BDC的面积为△ABC面积的两倍,
∴△BDC的高为△ABC高的两倍,
即D的纵坐标=±2×
=±
,
代入y=-
x+3得,±
=-
x+3,
解得x=-
或x=
,
∴D(-
,
),或(
,-
).
(3)设D(m,-
m+3),
∵B(-1,0),C(4,0).
∴BD2=(m+1)2+(-
m+3)2,CD2=(m-4)2+(-
m+3)2,
∵BD=CD,
∴(m+1)2+(-
m+3)2=(m-4)2+(-
m+3)2,解得m=
,
∴D(
,
).
∴
=
=
=
.
所以此时△ABD与△BCD的面积的比值为
.
|
解得
|
所以A(
| 8 |
| 7 |
| 15 |
| 7 |
令y=0,则x+1=0,解得x=-1,
则-
| 3 |
| 4 |
所以B(-1,0),C(4,0).
(2)∵△BDC的面积为△ABC面积的两倍,
∴△BDC的高为△ABC高的两倍,
即D的纵坐标=±2×
| 15 |
| 7 |
| 30 |
| 7 |
代入y=-
| 3 |
| 4 |
| 30 |
| 7 |
| 3 |
| 4 |
解得x=-
| 12 |
| 7 |
| 68 |
| 7 |
∴D(-
| 12 |
| 7 |
| 30 |
| 7 |
| 68 |
| 7 |
| 30 |
| 7 |
(3)设D(m,-
| 3 |
| 4 |
∵B(-1,0),C(4,0).
∴BD2=(m+1)2+(-
| 3 |
| 4 |
| 3 |
| 4 |
∵BD=CD,
∴(m+1)2+(-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
∴D(
| 3 |
| 2 |
| 15 |
| 8 |
∴
| S△ABD |
| S△BCD |
| S△ABC-S△BDC |
| S△BCD |
| ||||||||
|
| 1 |
| 7 |
所以此时△ABD与△BCD的面积的比值为
| 1 |
| 7 |
点评:本题考查了一次函数图象上点的坐标的特征,以及相交线的问题,利用两解析式联立求解交点坐标是常用的方法,需要熟练掌握并灵活运用.

练习册系列答案
相关题目
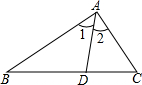 如图,∠1=∠2,∠C=2∠B,求证:AB=AC+CD.
如图,∠1=∠2,∠C=2∠B,求证:AB=AC+CD.