题目内容
3.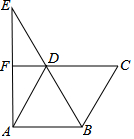 如图,在菱形ABCD中,延长BD到E使得BD=DE,连接AE,延长CD交AE于点F.
如图,在菱形ABCD中,延长BD到E使得BD=DE,连接AE,延长CD交AE于点F.(1)求证:AD=2DF;
(2)如果FD=2,∠C=60°,求菱形ABCD的面积.
分析 (1)直接利用菱形的性质结合三角形中位线定理得出AB=2DF,进而分析得出答案;
(2)首先得出,△DAB为等边三角形,进而利用已知得出DM的长,即可得出菱形ABCD的面积.
解答 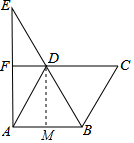 (1)证明:∵四边形ABCD是菱形,
(1)证明:∵四边形ABCD是菱形,
∴AD=AB,CD∥AB,
∵BD=DE,
∴EF=FA,
∴FD是△EAB的中位线,
∴AB=2FD,
∴AD=2FD;
(2)解:过点D作DM⊥AB,
∵FD=2,
∴AB=4,
∵∠C=60°,
∴∠ADB=∠60°,△DAB为等边三角形,
∴∠ADM=30°,AM=2,
∴DM=$\frac{AM}{tan60°}$,可得DM=2$\sqrt{3}$,
∴S菱形ABCD=AB•DM=4×2$\sqrt{3}$=8$\sqrt{3}$.
点评 此题主要考查了菱形的性质以及三角形中位线定理,正确得出△DAB为等边三角形是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知两点P1(1,y1),P2(5,y2)在反比例函数y=$\frac{5}{x}$的图象上,下列结论正确的是( )
| A. | 0<y1<y2 | B. | 0<y2<y1 | C. | y1<y2<0 | D. | y2<y1<0 |
18.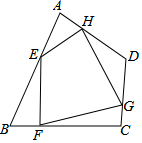 如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
 如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )| A. | 当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形 | |
| B. | 当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形 | |
| C. | 当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形 | |
| D. | 当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形 |
 如图,△ABC中,∠A=50°,∠B=70°,CD平分∠ACB,DE交AB于D交AC于E,∠CDE=30°,求∠ADE的度数.
如图,△ABC中,∠A=50°,∠B=70°,CD平分∠ACB,DE交AB于D交AC于E,∠CDE=30°,求∠ADE的度数. 如图,点E在菱形ABCD边上,AE=1,过E作AC的垂线EF,交AD于点M,交CD的延长线于点F,DF=2,∠B=60°,点P是AC上的动点,则PM+PF的最小值3$\sqrt{3}$.
如图,点E在菱形ABCD边上,AE=1,过E作AC的垂线EF,交AD于点M,交CD的延长线于点F,DF=2,∠B=60°,点P是AC上的动点,则PM+PF的最小值3$\sqrt{3}$.
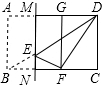 如图,在矩形ABCD中,AB=6,BC=8,点E是对角线BD上一动点(不与点B、D重合),将矩形沿过点E的直线MN折叠,使得点A、B的对应点G、F分别在直线AD与BC上,当△DEF为直角三角形时,CN的长为$\frac{25}{4}$或$\frac{7}{4}$.
如图,在矩形ABCD中,AB=6,BC=8,点E是对角线BD上一动点(不与点B、D重合),将矩形沿过点E的直线MN折叠,使得点A、B的对应点G、F分别在直线AD与BC上,当△DEF为直角三角形时,CN的长为$\frac{25}{4}$或$\frac{7}{4}$.