题目内容
20.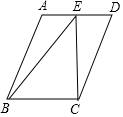 如图,面积为24的?ABCD中,BC=4,E是直线AD上一点,连接BE、CE,则sin∠BEC的最大值为$\frac{3}{5}$.
如图,面积为24的?ABCD中,BC=4,E是直线AD上一点,连接BE、CE,则sin∠BEC的最大值为$\frac{3}{5}$.
分析 因为面积为24的?ABCD中,BC=4,所以BC边上的高为6,由题意可知,当EB=EC时,∠BEC的值最大,作EH⊥BC于H,则BH=HC=2,EH=6,求出BM,BE,根据sin∠BEC=$\frac{BM}{EB}$计算即可.
解答 解: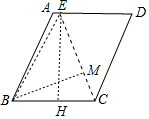 ∵面积为24的?ABCD中,BC=4,
∵面积为24的?ABCD中,BC=4,
∴BC边上的高为6,
由题意可知,当EB=EC时,∠BEC的值最大,
作EH⊥BC于H,则BH=HC=2,EH=6,
∴EB=EC=$\sqrt{E{H}^{2}+H{C}^{2}}$=2$\sqrt{10}$,
∵S△EBC=$\frac{1}{2}$•BC•EH=$\frac{1}{2}$•EC•BM,
∴BM=$\frac{6×4}{2\sqrt{10}}$=$\frac{6}{5}$$\sqrt{10}$,
在Rt△EBM中,sin∠BEC=$\frac{BM}{EB}$=$\frac{\frac{6}{5}\sqrt{10}}{2\sqrt{10}}$=$\frac{3}{5}$.
故答案为$\frac{3}{5}$.
点评 本题考查平行四边形的性质、解直角三角形、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
10.某商品的进价是500元,标价为750元,商店要求以利润不低于5%的售价打折出售,此商品最低可以打( )
| A. | 6折 | B. | 7折 | C. | 8折 | D. | 9折 |
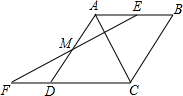 如图,点E在菱形ABCD边上,AE=1,过E作AC的垂线EF,交AD于点M,交CD的延长线于点F,DF=2,∠B=60°,点P是AC上的动点,则PM+PF的最小值3$\sqrt{3}$.
如图,点E在菱形ABCD边上,AE=1,过E作AC的垂线EF,交AD于点M,交CD的延长线于点F,DF=2,∠B=60°,点P是AC上的动点,则PM+PF的最小值3$\sqrt{3}$.
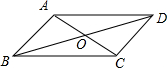 如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC:BD=1:2,
如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC:BD=1:2,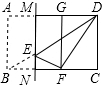 如图,在矩形ABCD中,AB=6,BC=8,点E是对角线BD上一动点(不与点B、D重合),将矩形沿过点E的直线MN折叠,使得点A、B的对应点G、F分别在直线AD与BC上,当△DEF为直角三角形时,CN的长为$\frac{25}{4}$或$\frac{7}{4}$.
如图,在矩形ABCD中,AB=6,BC=8,点E是对角线BD上一动点(不与点B、D重合),将矩形沿过点E的直线MN折叠,使得点A、B的对应点G、F分别在直线AD与BC上,当△DEF为直角三角形时,CN的长为$\frac{25}{4}$或$\frac{7}{4}$.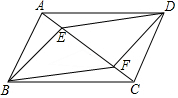 如图,在四边形ABCD中,AB∥CD,点E、F是对角线AC上两点,且∠ABF=∠CDE,AE=CF
如图,在四边形ABCD中,AB∥CD,点E、F是对角线AC上两点,且∠ABF=∠CDE,AE=CF 如图,点A在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当AC=1时,△ABC的周长为$\sqrt{3}$+1.
如图,点A在双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当AC=1时,△ABC的周长为$\sqrt{3}$+1.