题目内容
 已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )
已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )| A、30° | B、36° |
| C、50° | D、60° |
考点:翻折变换(折叠问题)
专题:
分析:首先证明∠ACN=∠ANC=2∠ACM,然后证明∠A=∠ACM即可解决问题.
解答: 解:由题意知:
解:由题意知:
∠ACM=∠NCM;
又∵AN=AC,
∴∠ACN=∠ANC=2∠ACM;
∵CM是直角△ABC的斜边AB上的中线,
∴CM=AM,
∴∠A=∠ACM;
由三角形的内角和定理知:
∠A+2∠A+2∠A=180°,
∴∠A=36°,
故选:B.
 解:由题意知:
解:由题意知:∠ACM=∠NCM;
又∵AN=AC,
∴∠ACN=∠ANC=2∠ACM;
∵CM是直角△ABC的斜边AB上的中线,
∴CM=AM,
∴∠A=∠ACM;
由三角形的内角和定理知:
∠A+2∠A+2∠A=180°,
∴∠A=36°,
故选:B.
点评:该命题考查了翻折变换及其应用问题;解题的关键是根据翻折变换的性质找出图形中隐含的等量关系;灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一元二次方程2x2-x-1=0的根的情况( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、无实数根 |
| D、无法确定 |
 如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )
如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )| A、无法确定 |
| B、8cm2 |
| C、16cm2 |
| D、4cm2 |
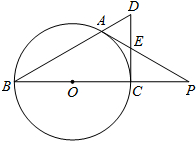 如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D.若CD的中点E,AE的延长线与BC的延长线交于点P.
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D.若CD的中点E,AE的延长线与BC的延长线交于点P.