题目内容
 如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )
如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )| A、无法确定 |
| B、8cm2 |
| C、16cm2 |
| D、4cm2 |
考点:旋转的性质,全等三角形的判定与性质,正方形的性质
专题:计算题
分析:如图,根据正方形的性质得OD=OC,∠ODA=∠OCD=45°,∠DOC=90°,再利用等角的余角相等得到∠DOE=∠COF,于是可根据“ASA”证明△ODE≌△OCF,
则S△ODE=S△OCF,所以S四边形EOFD=S△DOC=
S正方形ABCD.
则S△ODE=S△OCF,所以S四边形EOFD=S△DOC=
| 1 |
| 4 |
解答:解: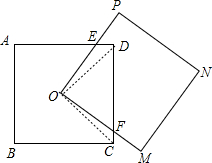 如图,
如图,
∵四边形ABCD为正方形,
∴OD=OC,∠ODA=∠OCD=45°,∠DOC=90°,
而∠POM=90°,
即∠DOF+∠COF=90°,∠DOE+∠DOF=90°,
∴∠DOE=∠COF,
在△ODE和△OCF中,
,
∴△ODE≌△OCF(ASA),
∴S△ODE=S△OCF,
∴S四边形EOFD=S△DOC=
S正方形ABCD=
×42=4(cm2).
故选D.
 如图,
如图,∵四边形ABCD为正方形,
∴OD=OC,∠ODA=∠OCD=45°,∠DOC=90°,
而∠POM=90°,
即∠DOF+∠COF=90°,∠DOE+∠DOF=90°,
∴∠DOE=∠COF,
在△ODE和△OCF中,
|
∴△ODE≌△OCF(ASA),
∴S△ODE=S△OCF,
∴S四边形EOFD=S△DOC=
| 1 |
| 4 |
| 1 |
| 4 |
故选D.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
 已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )
已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )| A、30° | B、36° |
| C、50° | D、60° |
 如图,直线a与直线c相交于点O,则∠1的度数是( )
如图,直线a与直线c相交于点O,则∠1的度数是( )| A、60° | B、50° |
| C、40° | D、30° |
 如图,A、B是函数y=kx与函数y=
如图,A、B是函数y=kx与函数y=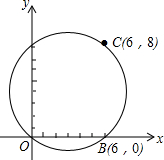 在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由这三个观测点确定的圆形区域是海洋生物保护区.
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由这三个观测点确定的圆形区域是海洋生物保护区.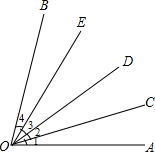 如图,∠1=∠2=∠3=∠4,根据图形回答:
如图,∠1=∠2=∠3=∠4,根据图形回答: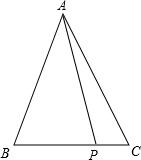 在△ABC中,AB=AC=5cm,P是BC边上一点,证明:无论底边BC的长度是多少,以及点P在BC上的位置如何,PA2+PB•PC的值总是常数.
在△ABC中,AB=AC=5cm,P是BC边上一点,证明:无论底边BC的长度是多少,以及点P在BC上的位置如何,PA2+PB•PC的值总是常数.