题目内容
20.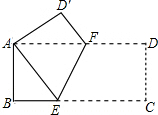 如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则AF的长为( )
如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则AF的长为( )| A. | 4$\sqrt{5}$ | B. | 8 | C. | 6 | D. | 10 |
分析 由平行线的性质可知∠AFE=∠FEC,由翻折的性质可知∠AEF=∠CEF,AE=EC,从而得到∠AEF=∠AFE,从而得到AF=AE,最后在△ABE中利用勾股定理求解即可.
解答 解:∵AD∥BC,
∴∠AFE=∠FEC.
由翻折的性质可知:∠AEF=∠CEF,AE=EC.
∴∠AEF=∠AFE.
∴AF=AE.
设EC=x,则AE=AF=x,BE=16-x.
在Rt△ABE中,由勾股定理得:AE2=AB2+BE2,即x2=82+(16-x)2,
解得:x=10.
∴AF=10.
故选:D.
点评 本题主要考查的是翻折的性质、矩形的性质、勾股定理的应用,利用勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
11.下列运算中结果正确的是( )
| A. | -3x+5x=-8x | B. | 5y-3y=2 | C. | 3x2y-2x2y=x2y | D. | 3a+2b=5ab |
15.求$\frac{49}{81}$的平方根的数学表达式为( )
| A. | $\sqrt{\frac{49}{81}}$=±$\frac{7}{9}$ | B. | $\sqrt{\frac{49}{81}}$=-$\frac{7}{9}$ | C. | ±$\sqrt{\frac{49}{81}}$=±$\frac{7}{9}$ | D. | $\sqrt{\frac{49}{81}}$=$\frac{7}{9}$ |
 如图,在Rt△ABC中,∠A,∠B,∠C的对边分别是a,b,c.证明:sin2A+cos2A=1.
如图,在Rt△ABC中,∠A,∠B,∠C的对边分别是a,b,c.证明:sin2A+cos2A=1.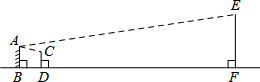 如图,小明在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为7m.
如图,小明在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为7m.