题目内容
如图，水库大坝的横断面是梯形，坝顶宽BC=10米，坝高BE=CF=30米，斜坡AB的坡角∠A=30°，斜坡CD的坡度i=1：3，求坝底宽AD的长．（结果保留根号）考点：解直角三角形的应用-坡度坡角问题
专题：
分析：在Rt△DCF中利用DC的坡度和CF的长求得线段DF的长，然后与AE、EF相加即可求得AB的长．
解答：解：∵坝高BE=CF=30米，斜坡AB的坡角∠A=30°，
∴tan30°=
=
，
∴AE=30
（m），
∵斜坡CD的坡度i=1：3，
∴DF=3×30=90（m），
∴AD=AE+EF=DF=30
+10+90=（100+30
）m，
答：坝底宽AD的长为（100+30
）m．
∴tan30°=
| BE |
| AE |
| ||
| 3 |
∴AE=30
| 3 |
∵斜坡CD的坡度i=1：3，
∴DF=3×30=90（m），
∴AD=AE+EF=DF=30
| 3 |
| 3 |
答：坝底宽AD的长为（100+30
| 3 |
点评：本题考查了坡度、坡角的知识，解答本题的关键是理解掌握坡度、坡角的定义，能正确解直角三角形．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
如图，在△ABC中，∠A=60°，∠B=70°，∠ACB的平分线交AB于D，DE∥BC交AC于E，求∠BDC、∠EDC．下列命题是假命题的是（ ）
| A、互补的两个角不能都是锐角 |
| B、若a⊥b，a⊥c，则b⊥c |
| C、斜边和一条直角边分别相等的两个三角形全等 |
| D、全等三角形的对应角相等 |
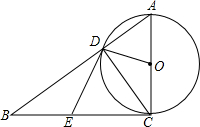如图，以△ABC的边AC为直径的⊙O与BC相切于点C，⊙O与AB相交于点D，E是BC的中点．