题目内容
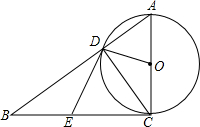 如图,以△ABC的边AC为直径的⊙O与BC相切于点C,⊙O与AB相交于点D,E是BC的中点.
如图,以△ABC的边AC为直径的⊙O与BC相切于点C,⊙O与AB相交于点D,E是BC的中点.(1)求证:DE是⊙O的切线;
(2)若⊙O的直径为5,
| AD |
| CD |
| 1 |
| 2 |
考点:切线的判定与性质
专题:
分析:(1)连接OD.欲证ED与⊙O相切,只需证明OD⊥DE;
(2)通过相似三角形△ADC∽△CDB的对应边成比例知
=
,由此可以求得线段BC的长度,根据直角三角形斜边中线的性质即可求得.
(2)通过相似三角形△ADC∽△CDB的对应边成比例知
| BC |
| AC |
| DC |
| AD |
解答: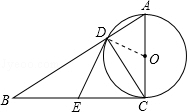 (1)证明:连接OD.
(1)证明:连接OD.
∵BC是⊙O⊙的切线,AC是直径,
,∴∠ACB=90°,
∵AC是直径,
∴∠ADC=90°,
∴∠CDB=90°,
又∵EB=EC
∴DE为直角△DCB斜边的中线,
∴DE=CE=
BC.
∴∠DCE=∠CDE,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°,
∴∠ODE=90°
∴DE是⊙O的切线.
(2)∵
=
,
∴设AD=x,CD=2x,
∵AC=5,AD2+DC2=AC2,
∴x2+(2x)2=52,
∴x=1,
即AD=1,CD=2,
在Rt△BDC和Rt△ADC中,∠ADC=∠BDC=90°,∠ABC=90°,
∴∠ABC+∠A=90°,∠ABC+∠BCD=90°,
∴∠A=∠BCD,
∵△ADC∽△CDB,
∴
=
,
即
=
,
∴BC=10.
∴DE=
BC=5.
 (1)证明:连接OD.
(1)证明:连接OD.∵BC是⊙O⊙的切线,AC是直径,
,∴∠ACB=90°,
∵AC是直径,
∴∠ADC=90°,
∴∠CDB=90°,
又∵EB=EC
∴DE为直角△DCB斜边的中线,
∴DE=CE=
| 1 |
| 2 |
∴∠DCE=∠CDE,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°,
∴∠ODE=90°
∴DE是⊙O的切线.
(2)∵
| AD |
| CD |
| 1 |
| 2 |
∴设AD=x,CD=2x,
∵AC=5,AD2+DC2=AC2,
∴x2+(2x)2=52,
∴x=1,
即AD=1,CD=2,
在Rt△BDC和Rt△ADC中,∠ADC=∠BDC=90°,∠ABC=90°,
∴∠ABC+∠A=90°,∠ABC+∠BCD=90°,
∴∠A=∠BCD,
∵△ADC∽△CDB,
∴
| BC |
| AC |
| DC |
| AD |
即
| BC |
| 5 |
| 2 |
| 1 |
∴BC=10.
∴DE=
| 1 |
| 2 |
点评:本题考查了相似三角形的判定与性质、切线的判定与性质.圆心到一条直线的距离等于该圆的半径,则该直线就是圆的一条切线.

练习册系列答案
相关题目
已知圆锥的底面半径为6cm,高为8cm,圆锥的侧面积为( )
| A、48π | B、96π |
| C、30π | D、60π |
下列命题的逆命题是真命题的是( )
| A、直角都相等 |
| B、等边三角形是锐角三角形 |
| C、相等的角是对顶角 |
| D、全等三角形的对应角相等 |
把二次函数y=2x2-1的图象向上平移3个单位所得二次函数图象的函数关系式为( )
| A、y=2(x-3)2+1 |
| B、y=2(x+3)2+1 |
| C、y=2x2+2 |
| D、y=2x2-4 |
 如图,水库大坝的横断面是梯形,坝顶宽BC=10米,坝高BE=CF=30米,斜坡AB的坡角∠A=30°,斜坡CD的坡度i=1:3,求坝底宽AD的长.(结果保留根号)
如图,水库大坝的横断面是梯形,坝顶宽BC=10米,坝高BE=CF=30米,斜坡AB的坡角∠A=30°,斜坡CD的坡度i=1:3,求坝底宽AD的长.(结果保留根号) 已知:如图所示,△ABC中,AD⊥BC,AB=AE,点E在AC的垂直平分线上.
已知:如图所示,△ABC中,AD⊥BC,AB=AE,点E在AC的垂直平分线上.