题目内容
20.如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
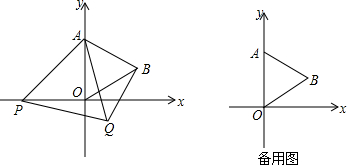
分析 (1)如图,作辅助线;证明∠BOC=30°,OB=2,借助直角三角形的边角关系即可解决问题;
(2)证明△APO≌△AQB,得到∠ABQ=∠AOP=90°,即可解决问题;
(3)根据点P在x的正半轴还是负半轴两种情况讨论,再根据全等三角形的性质即可得出结果.
解答 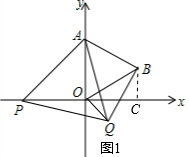 解:(1)如图1,过点B作BC⊥x轴于点C,
解:(1)如图1,过点B作BC⊥x轴于点C,
∵△AOB为等边三角形,且OA=2,
∴∠AOB=60°,OB=OA=2,
∴∠BOC=30°,而∠OCB=90°,
∴BC=$\frac{1}{2}$OB=1,OC=$\sqrt{3}$,
∴点B的坐标为B($\sqrt{3}$,1);
(2)∠ABQ=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ、AO=AB、∠PAQ=∠OAB,
∴∠PAO=∠QAB,
在△APO与△AQB中,
$\left\{\begin{array}{l}{AP=AQ}\\{∠PAO=∠QAB}\\{AO=AB}\end{array}\right.$,
∴△APO≌△AQB(SAS),
∴∠ABQ=∠AOP=90°;
(3)当点P在x轴负半轴上时,点Q在点B的下方,
∵AB∥OQ,∠BQO=90°,∠BOQ=∠ABO=60°.
又OB=OA=2,可求得BQ=$\sqrt{3}$,
由(2)可知,△APO≌△AQB,
∴OP=BQ=$\sqrt{3}$,
∴此时P的坐标为(-$\sqrt{3}$,0).
点评 本题主要考查了等边三角形的性质以及全等三角形的判定及性质以及梯形的性质,注意利用分类讨论得出是解题关键.

练习册系列答案
相关题目
10.学校捐资购买了一批物资120吨打算支援山区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
(2)为了节省运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
8.$\frac{3}{2}$的相反数是( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
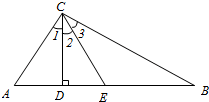 已知,如图,△ABC中,CD,CE分别是AB边上的高和中线,且∠1=∠2=∠3,求△ABC各内角的度数.
已知,如图,△ABC中,CD,CE分别是AB边上的高和中线,且∠1=∠2=∠3,求△ABC各内角的度数.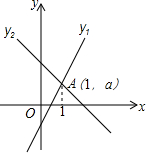 (1)计算:$\frac{2}{1+tan60°}$+|$\sqrt{3}$-2|
(1)计算:$\frac{2}{1+tan60°}$+|$\sqrt{3}$-2|
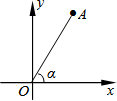 如图,点A(3,t)在第一象限,OA与x轴所夹的锐角为α,tanα=$\frac{3}{2}$,则t的值是$\frac{9}{2}$.
如图,点A(3,t)在第一象限,OA与x轴所夹的锐角为α,tanα=$\frac{3}{2}$,则t的值是$\frac{9}{2}$.