题目内容
5.(1)化简:($\frac{1}{a-b}$-$\frac{1}{a+b}$)÷$\frac{b}{{a}^{2}-2ab+{b}^{2}}$(2)解不等式组$\left\{\begin{array}{l}{2x>-3}\\{x-1≤8-2x}\end{array}\right.$;并求它的最小整数解.
分析 (1)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,找出最小的整数解即可.
解答 解:(1)原式=$\frac{a+b-a+b}{(a+b)(a-b)}$•$\frac{(a-b)^{2}}{b}$=$\frac{2(a-b)}{a+b}$;
(2)$\left\{\begin{array}{l}{2x>-3①}\\{x-1≤8-2x②}\end{array}\right.$
解不等式①得:x>-$\frac{3}{2}$;
解不等式②得:x≤3,
∴不等式组的解集是:-$\frac{3}{2}$<x≤3,
则最小整数解是:x=-1.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.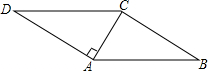 在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是( )
在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是( )
 在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是( )
在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是( )| A. | 4+2$\sqrt{3}$ | B. | 8 | C. | 8+4$\sqrt{3}$ | D. | 16 |
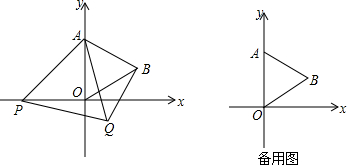
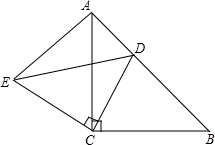 已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为线段AB上一动点.
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为线段AB上一动点.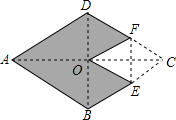 如图,菱形ABCD中,AC与BD相交于点O.将菱形沿EF折叠,使点C与点O重合.若AC=8,BD=6,则图中阴影部分的面积为18.
如图,菱形ABCD中,AC与BD相交于点O.将菱形沿EF折叠,使点C与点O重合.若AC=8,BD=6,则图中阴影部分的面积为18.