题目内容
10.学校捐资购买了一批物资120吨打算支援山区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
(2)为了节省运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
分析 (1)设需甲车x辆,乙车y辆列出方程组即可.
(2)设甲车有a辆,乙车有b辆,则丙车有(14-a-b)辆,列出等式.
解答 解:(1)设需甲车x辆,乙车y辆,根据题意得
$\left\{\begin{array}{l}{5x+8y=120}\\{400x+500y=8200}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=8}\\{y=10}\end{array}\right.$.
答:需甲种车型为8辆,乙种车型为10辆.
(2)设甲车有a辆,乙车有b辆,则丙车有(14-a-b)辆,由题意得
5a+8b+10(14-a-b)=120,
化简得5a+2b=20,
即a=4-$\frac{2}{5}$b,
∵a、b、14-a-b均为正整数,
∴b只能等于5,从而a=2,14-a-b=7,
∴甲车2辆,乙车5辆,丙车7辆,
∴需运费400×2+500×5+600×7=7500(元).
答:甲车2辆,乙车5辆,丙车7辆,需运费7500元.
点评 本题考查二元一次方程组的应用,一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出方程即可求解.利用整体思想和未知数的实际意义通过筛选法可得到未知数的具体解,这种方法要掌握.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
19.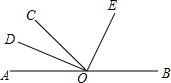 ∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.
∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.
 ∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.
∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.| A. | 60° | B. | 65° | C. | 90° | D. | 80° |
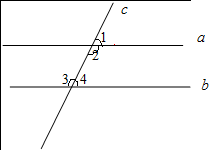 如图,因为a∥b,所以∠1=∠4,理由是两直线平行,同位角相等.
如图,因为a∥b,所以∠1=∠4,理由是两直线平行,同位角相等.