题目内容
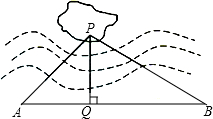如图，湖中有一孤立小岛，湖边有一条笔直的观光小道AB，现从小岛架一座与观光小道垂直的小桥PQ，已知∠A=45゜，∠B=30゜，AB=60米，小桥PD的长为考点：解直角三角形的应用
专题：
分析：设PQ=x米，在直角△PAQ和直角△PBQ中分别利用x表示出AQ和BQ的长，根据AB=AQ+BQ，即可列方程求得x的值．
解答：解：设PQ=x米，
在直角△PAQ中，tan∠A=
，
∴AQ=
=x，
在直角△PBQ中，tan∠B=
，
∴BQ=
=
x，
∵AB=100米，
∴x+
x=100，
解得：x=50
-50．
即：小桥PQ的长度约是（50
-50）米．
故答案是：50
-50．
在直角△PAQ中，tan∠A=
| x |
| AQ |
∴AQ=
| x |
| tan45° |
在直角△PBQ中，tan∠B=
| x |
| bQ |
∴BQ=
| x |
| tan30° |
| 3 |
∵AB=100米，
∴x+
| 3 |
解得：x=50
| 3 |
即：小桥PQ的长度约是（50
| 3 |
故答案是：50
| 3 |
点评：本题考查了解直角三角形的应用，解答本题的关键是构造直角三角形，利用三角函数表示出相关线段的长度，难度一般．
练习册系列答案
高效智能课时作业系列答案
相关题目
要得到抛物线y=2（x-4）2-1，可以将抛物线y=2x2（ ）
| A、向右平移4个单位长度，再向下平移1个单位长度 |
| B、向右平移4个单位长度，再向上平移1个单位长度 |
| C、向左平移4个单位长度，再向下平移1个单位长度 |
| D、向左平移4个单位长度，再向上平移1个单位长度 |
比x和y2的差的一半大5的数可表示为（ ）
A、
| ||
B、
| ||
| C、（x-y2）+5 | ||
| D、（x-y2）-5 |
若某件商品的原价为a元，提价10%后，欲恢复原价，应降价（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|