题目内容
[a]表示不大于a的最大整数，那么方程[2x+1]=3x-1的实根是 ．
考点：取整计算
专题：
分析：由[a]表示不大于a的最大整数可知a-1＜[a]≤a，由此得到2x＜[2x+1]≤2x+1即2x＜3x-1≤2x+1，从而求出3x的范围．由于[2x+1]是整数，因此3x是整数，根据3x的范围就可得到整数3x的值，就可解决问题．
解答：解：∵[a]表示不大于a的最大整数，
∴a-1＜[a]≤a，
∴2x＜[2x+1]≤2x+1．
∵[2x+1]=3x-1，
∴2x＜3x-1≤2x+1．
解得：1＜x≤2，
∴3＜3x≤6．
∵[2x+1]是整数，∴3x是整数，
∴3x可取4、5、6．
∴x可取
、
、2．
故答案为：x=
或x=
或x=2．
∴a-1＜[a]≤a，
∴2x＜[2x+1]≤2x+1．
∵[2x+1]=3x-1，
∴2x＜3x-1≤2x+1．
解得：1＜x≤2，
∴3＜3x≤6．
∵[2x+1]是整数，∴3x是整数，
∴3x可取4、5、6．
∴x可取
| 4 |
| 3 |
| 5 |
| 3 |
故答案为：x=
| 4 |
| 3 |
| 5 |
| 3 |
点评：本题考查了取整计算、解不等式组、求整数解等知识，理解[a]的含义（即a-1＜[a]≤a）是解决本题的关键．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
下列各式中正确的是（ ）
A、
| ||||||
B、（-
| ||||||
C、
| ||||||
D、-
|
如图所示，写出△ABC各顶点的坐标以及△ABC关于x对称的△A1B1C1的各顶点坐标，并画出△ABC关于y对称的△A2B2C2．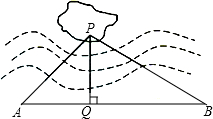
如图，湖中有一孤立小岛，湖边有一条笔直的观光小道AB，现从小岛架一座与观光小道垂直的小桥PQ，已知∠A=45゜，∠B=30゜，AB=60米，小桥PD的长为
如图，已知梯形的下底为a，半圆的半径为r．