题目内容
解下列方程:
(1)x2-3x=2
(2)x2-5x+6=0
(3)(3x+1)2=4(x-2)2.
(1)x2-3x=2
(2)x2-5x+6=0
(3)(3x+1)2=4(x-2)2.
考点:解一元二次方程-因式分解法,解一元二次方程-公式法
专题:计算题
分析:(1)先把方程化为一般式,然后根据求根公式法解方程;
(2)利用因式分解法解方程;
(3)先移项得到(3x+1)2-4(x-2)2=0,然后利用因式分解法解方程.
(2)利用因式分解法解方程;
(3)先移项得到(3x+1)2-4(x-2)2=0,然后利用因式分解法解方程.
解答:解:(1)x2-3x-2=0,
△=(-3)2-4×1×(-2)=17,
所以x=
,
所以x1=
,x2=
;
(2)(x-2)(x-3)=0,
x-2=0或x-3=0,
所以x1=2,x2=3;
(3)(3x+1)2-4(x-2)2=0,
(3x+1+2x-4)(3x+1-2x+4)=0,
3x+1+2x-4=0或3x+1-2x+4=0,
所以x1=
,x2=-5.
△=(-3)2-4×1×(-2)=17,
所以x=
3±
| ||
| 2×1 |
所以x1=
3+
| ||
| 2 |
3-
| ||
| 2 |
(2)(x-2)(x-3)=0,
x-2=0或x-3=0,
所以x1=2,x2=3;
(3)(3x+1)2-4(x-2)2=0,
(3x+1+2x-4)(3x+1-2x+4)=0,
3x+1+2x-4=0或3x+1-2x+4=0,
所以x1=
| 3 |
| 5 |
点评:本题考查了解一元二次方程-因式分解法:因式分解法解一元二次方程的一般步骤:移项,使方程的右边化为零;将方程的左边分解为两个一次因式的乘积;令每个因式分别为零,得到两个一元一次方程;解这两个一元一次方程,它们的解就都是原方程的解.也考查了公式法解一元二次方程.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
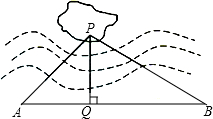 如图,湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现从小岛架一座与观光小道垂直的小桥PQ,已知∠A=45゜,∠B=30゜,AB=60米,小桥PD的长为
如图,湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现从小岛架一座与观光小道垂直的小桥PQ,已知∠A=45゜,∠B=30゜,AB=60米,小桥PD的长为 已知,在平面直角坐标系中,AB是双曲线y=
已知,在平面直角坐标系中,AB是双曲线y= 有一架5米长的梯子搭在墙上,刚好与墙 头对齐,此时梯脚与墙的距离是3米,
有一架5米长的梯子搭在墙上,刚好与墙 头对齐,此时梯脚与墙的距离是3米, 图中△ABC的外心坐标是
图中△ABC的外心坐标是