题目内容
已知点A（x1，y1），B（x2，y2）在二次函数y=x2-6x+4的图象上，若x1＜x2＜3，则y1 y2（填“＞”、“=”或“＜”）．
考点：二次函数图象上点的坐标特征
专题：计算题
分析：先利用配方法得到抛物线的对称轴，然后根据二次函数的性质求解．
解答：解：y=x2-6x+4=（x-3）2-5，
抛物线的对称轴为直线x=3，而抛物线开口向上，
所以当x1＜x2＜3，y1＞y2．
故答案为：＞．
抛物线的对称轴为直线x=3，而抛物线开口向上，
所以当x1＜x2＜3，y1＞y2．
故答案为：＞．
点评：本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了二次函数的性质．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
如图，已知二次函数y=a（x-h）2+2| 3 |
（1）写出该函数图象的对称轴；
（2）若将线段OA绕点O逆时针旋转60°到OA′，试判断点A′是否为该函数图象的顶点？
如图所示△ABC中，点D，E在边AB上且满足AD=AC，BE=BC，若∠ACB=128°，那么∠DCE的度数为下列各式中正确的是（ ）
A、
| ||||||
B、（-
| ||||||
C、
| ||||||
D、-
|
（-
）2015×
=（ ）
| 5 |
| 2 |
| 22016+62016 |
| 52016+152016 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
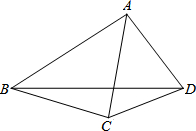如图，在四边形ABCD中，对角线AC平分∠BAD，AB＞AC，下列结论正确的是（ ）| A、AB-AD＞CB-CD |
| B、AB-AD=CB-CD |
| C、AB-AD＜CB-CD |
| D、AB-AD与CB-CD的大小关系不确定 |
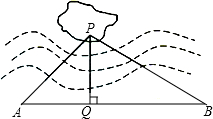如图，湖中有一孤立小岛，湖边有一条笔直的观光小道AB，现从小岛架一座与观光小道垂直的小桥PQ，已知∠A=45゜，∠B=30゜，AB=60米，小桥PD的长为