题目内容
14.直线y=kx+b与抛物线y=$\frac{1}{4}$x2交于A(x1,y1)、B(x2,y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为(0,4).分析 根据直线y=kx+b与抛物线y=$\frac{1}{4}$x2交于A(x1,y1)、B(x2,y2)两点,可以联立在一起,得到关于x的一元二次方程,从而可以得到两根之和与两根之积,再根据OA⊥OB,可以求得b的值,从而可以得到直线AB恒过的定点的坐标.
解答 解:∵直线y=kx+b与抛物线y=$\frac{1}{4}$x2交于A(x1,y1)、B(x2,y2)两点,
∴kx+b=$\frac{1}{4}{x}^{2}$,
化简,得 x2-4kx-4b=0,
∴x1+x2=4k,x1x2=-4b,
又∵OA⊥OB,
∴$\frac{{y}_{1}-0}{{x}_{1}-0}•\frac{{y}_{2}-0}{{x}_{2}-0}=\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}=\frac{\frac{1}{4}{{x}_{1}}^{2}•\frac{1}{4}{{x}_{2}}^{2}}{{x}_{1}{x}_{2}}=\frac{{x}_{1}{x}_{2}}{16}$=$\frac{-4b}{16}=-1$,
解得,b=4,
即直线y=kx+4,故直线恒过顶点(0,4),
故答案为:(0,4).
点评 本题考查二次函数的性质、一次函数的性质,解题的关键是明确题意,找出所求问题需要的条件,知道两条直线垂直时,它们解析式中的k的乘积为-1.

练习册系列答案
相关题目
4.为了了解开展“尊敬父母,从家务事做起”活动的实施情况,某校抽取八年级某班50名学生,调查他们一周做家务所用的时间,得到一组数据,并绘制制成下表,请根据下表完成下列各题:
(1)填写表中未完成的部分;
(2)这组数据的中位数是2.5小时,众数是3小时;
(3)该班学生每周做家务的平均时间是多少小时(写出计算的过程)
| 每周做家务的时间(小时) | 0 | 1 | 2 | 3 | 4 | 合计 |
| 人数 | 2 | 6 | 17 | 20 | 5 | 50 |
(2)这组数据的中位数是2.5小时,众数是3小时;
(3)该班学生每周做家务的平均时间是多少小时(写出计算的过程)
2.雾霾天气影响着我国北方中东部地区,给人们的健康带来严重的危害,为了让人们更好地了解雾霾,张超通过显微镜,将空气中细小的霾颗粒放大1000倍,发现这些霾颗粒平均值约为15微米,其中15微米(1米=1000000微米)用科学记数法可表示为( )
| A. | 1.5×105米 | B. | 0.15×10-1米 | C. | 1.5×10-5米 | D. | 15×10-6米 |
6.|-2016|的相反数是( )
| A. | $\frac{1}{2016}$ | B. | -2016 | C. | $-\frac{1}{2016}$ | D. | 2016 |
3.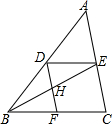 如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
 如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )| A. | $\frac{AD}{DB}$=$\frac{AE}{EC}$ | B. | $\frac{DE}{BC}$=$\frac{AE}{EC}$ | C. | $\frac{DE}{BF}$=$\frac{AE}{EC}$ | D. | $\frac{EH}{HB}$=$\frac{AE}{EC}$ |
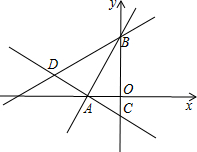 如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根
如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根