题目内容
5.若不等式5(x-2)+8≤6(x-1)+7的最小整数解是方程3x-ax=-3的解,求4a-$\frac{14}{a}$的值.分析 解不等式求出x的范围,从而得出不等式的最小整数解,代入方程求得a的值,最后代入代数式求值即可.
解答 解:去括号,得:5x-10+8≤6x-6+7,
移项、合并,得:-x≤3,
系数化为1,得:x≥-3,
∴不等式的最小整数解为-3,
代入方程3x-ax=-3,得:-9+3a=-3,
解得:a=2,
则原式=8-7=1.
点评 本题考查的是解一元一次不等式和一元一次方程及代数式的求值,正确求出每一个不等式解集是基础得出a的值是解答此题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
8.为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如下数据:
(1)该轿车油箱的容量为50L,行驶100km时,油箱剩余油量为42L;
(2)根据上表的数据,写出油箱剩余油量w(L)与轿车行驶的路程s(km)之间的表达式w=50-0.08s;
(3)某人将油箱加满后,驾驶该轿车从A地前往B地,到达B地时邮箱剩余油量为26L,求A,B两地之间的距离.
| 轿车行驶的路程s(km) | 0 | 10 | 20 | 30 | 40 | … |
| 油箱剩余油量w(L) | 50 | 49.2 | 48.4 | 47.6 | 46.8 | … |
(2)根据上表的数据,写出油箱剩余油量w(L)与轿车行驶的路程s(km)之间的表达式w=50-0.08s;
(3)某人将油箱加满后,驾驶该轿车从A地前往B地,到达B地时邮箱剩余油量为26L,求A,B两地之间的距离.
15.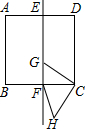 如图,正方形ABCD的边长为6,EF为正方形ABCD的对称轴,交BC于F点,点G是对称轴EF上的一个动点,连接GC,将线段GC绕点C逆时针旋转90°得到HC,连接HF,则在点G运动过程中,HF的最小值是( )
如图,正方形ABCD的边长为6,EF为正方形ABCD的对称轴,交BC于F点,点G是对称轴EF上的一个动点,连接GC,将线段GC绕点C逆时针旋转90°得到HC,连接HF,则在点G运动过程中,HF的最小值是( )
 如图,正方形ABCD的边长为6,EF为正方形ABCD的对称轴,交BC于F点,点G是对称轴EF上的一个动点,连接GC,将线段GC绕点C逆时针旋转90°得到HC,连接HF,则在点G运动过程中,HF的最小值是( )
如图,正方形ABCD的边长为6,EF为正方形ABCD的对称轴,交BC于F点,点G是对称轴EF上的一个动点,连接GC,将线段GC绕点C逆时针旋转90°得到HC,连接HF,则在点G运动过程中,HF的最小值是( )| A. | $\frac{1}{2}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3 |
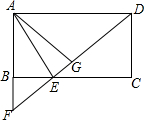 如图,四边形ABCD是矩形,点E在线段CB上,连接DE交AB的延长线于点F,∠AED=2∠CED,点G是DF中点,若BE=2,AG=2$\sqrt{7}$,则AB的长为2$\sqrt{6}$.
如图,四边形ABCD是矩形,点E在线段CB上,连接DE交AB的延长线于点F,∠AED=2∠CED,点G是DF中点,若BE=2,AG=2$\sqrt{7}$,则AB的长为2$\sqrt{6}$.