题目内容
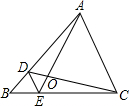
9．
已知：A、B、C、D四点均在⊙O上，点E在CD的延长线上，AB=AC．求证：DA平分∠BDE．
分析 根据圆周角定理和圆内接四边形的性质得到∠ADE=∠ABC，∠ADB=∠ACB，由等腰三角形的性质得到∠ACB=∠ABC，等量代换得到∠ADE=∠ADB，于是得到结论．
解答 证明：∵A，B，C，D四点共圆，
∴∠ADE=∠ABC，∠ADB=∠ACB，
∵AC=BA，
∴∠ACB=∠ABC，
∴∠ADE=∠ADB，
∴DA平分∠BDE．
点评 本题考查了圆周角定理，圆内接四边形的性质，角平分线的判定，熟练掌握圆周角定理是解题的关键．
练习册系列答案
相关题目
20．用四舍五入法将5109500取近似值（精确到万位），正确的是（ ）
| A． | 510 | B． | 5.11×106 | C． | 5.10×106 | D． | 5100000 |
如图，一共有15条线段，有10个三角形．
18．
如图，D、E分别是△ABC边AB、BC上的点，DE∥AC，若S△BDE：S△CDE=1：3，则$\frac{DE}{AC}$的值为（ ）
如图，D、E分别是△ABC边AB、BC上的点，DE∥AC，若S△BDE：S△CDE=1：3，则$\frac{DE}{AC}$的值为（ ）| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |