题目内容
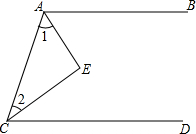 如图,AE平分∠BAC,CE平分∠ACD,要使AB∥CD,则∠1和∠2应满足的条件是
如图,AE平分∠BAC,CE平分∠ACD,要使AB∥CD,则∠1和∠2应满足的条件是考点:平行线的判定
专题:
分析:根据两直线平行,同旁内角互补可得∠BAC+∠ACD=180°,再根据角平分线的定义求出∠EAC+∠ECA=90°,然后求出∠E=90°,即可求得∠1和∠2的关系.
解答:证明:∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵AE平分∠BAC,CE平分∠ACD,
∴∠EAC+∠ECA=
(∠BAC+∠ACD)=90°,
∴∠E=90°,
则∠1+∠2=90°.
故答案是:∠1和∠2互余.
∴∠BAC+∠ACD=180°,
∵AE平分∠BAC,CE平分∠ACD,
∴∠EAC+∠ECA=
| 1 |
| 2 |
∴∠E=90°,
则∠1+∠2=90°.
故答案是:∠1和∠2互余.
点评:本题考查了平行线的性质,角平分线的定义,垂直的定义,熟记性质与概念是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图几何体的主视图是( )
如图几何体的主视图是( )A、 |
B、 |
C、 |
D、 |
下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )
| A、3、4、5 |
| B、6、8、10 |
| C、1、2、3 |
| D、5、12、13 |
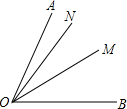 (1)如图,∠AOB的平分线为OM,0N为∠AOM内的一条射线,若∠BON=57°,∠AON=11°时,求∠MON的度数;
(1)如图,∠AOB的平分线为OM,0N为∠AOM内的一条射线,若∠BON=57°,∠AON=11°时,求∠MON的度数;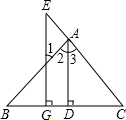 如图所示,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1,试说明AD平分∠BAC.下面是部分推理过程,请你将其补充完整:
如图所示,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1,试说明AD平分∠BAC.下面是部分推理过程,请你将其补充完整: 如图所示,在直角△ABC中,已知∠C=90°,AB=10cm,BC=8cm,AC=6cm,点P从点A出发以3cm/s的速度经过点B向点C运动,同时,点Q从点B出发以2cm/s的速度向点C运动,设运动时间为t(s).
如图所示,在直角△ABC中,已知∠C=90°,AB=10cm,BC=8cm,AC=6cm,点P从点A出发以3cm/s的速度经过点B向点C运动,同时,点Q从点B出发以2cm/s的速度向点C运动,设运动时间为t(s). 如图,∠AOB=∠COD=90°,OC平分∠AOB,∠DOE:∠BOE=2:3,试求∠COE的度数.
如图,∠AOB=∠COD=90°,OC平分∠AOB,∠DOE:∠BOE=2:3,试求∠COE的度数.