Question

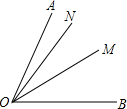（1）如图，∠AOB的平分线为OM，0N为∠AOM内的一条射线，若∠BON=57°，∠AON=11°时，求∠MON的度数；
（2）某同学经过认真的分析，得出一个关系式：∠MON=

1

2

（∠BON-∠AON），你认为这个同学得出的关系式是正确的吗？若正确，请把得出这个结论的过程写出来．

Answer 1

考点：角平分线的定义

专题：

分析：（1）先由角平分线定义可得∠AOM=

1

2

∠AOB=

1

2

（∠BON+∠AON）=

1

2

×68°=34°，再根据∠MON=∠AOM-∠AON，代入数据计算即可；
（2）先由角平分线定义可得∠AOM=∠BOM，再根据∠AOM=∠AON+∠MON，∠MON=∠BON-∠MON即可解题．

解答：解：（1）∵OM平分∠AOB，
∴∠AOM=

1

2

∠AOB=

1

2

（∠BON+∠AON）=

1

2

×68°=34°，
∴∠MON=∠AOM-∠AON=34°-11°=23°；

（2）∵OM平分∠AOB，
∴∠AOM=∠BOM，
∵∠AON+∠MON=∠BON-∠MON，
∴2∠MON=∠BON-∠AON，
∴∠MON=

1

2

（∠BON-∠AON），
因此这个同学得出的关系式正确．

点评：本题考查了角平分线定义，角的和与差的计算，（2）中求得∠AON+∠MON=∠BON-∠MON是解题的关键．