题目内容
11.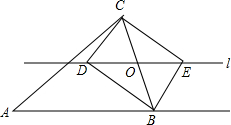 如图,∠CBF是△ABC的一个外角,点O是BC上的任意一点(不与B、C重合),过点O作直线l∥AB,且直线l与∠ABC的平分线相交于D,与∠CBF的平分线相交于E,
如图,∠CBF是△ABC的一个外角,点O是BC上的任意一点(不与B、C重合),过点O作直线l∥AB,且直线l与∠ABC的平分线相交于D,与∠CBF的平分线相交于E,(1)OD与OE是否相等?为什么?
(2)若BD=2,BE=5,求OB的长;
(3)当O在何处时,四边形BDCE为矩形?并说明理由?
分析 (1)要说明OD、OE相等,需找到一个中间量(OB),把它们连接起来.已知BD、BE分别是角平分线,l与AB平行,可根据角平分线、平行线的性质,说明∠BDE=∠CBD,∠BED=∠CBE,利用等角对等边解决.
(2)由于BD、BE分别是∠ABC、∠CBF的角平分线,而∠ABC和∠CBF是邻补角,易证明∠DBE是直角,利用勾股定理求出DE,通过直角三角形斜边中线与斜边关系,求出BO.
(3)由(2)知∠DBE是直角,若四边形BDCE为矩形,尚缺四边形BDCE为平行四边形的条件.由(1)知O是对角线DE的中点,若O是BC的中点时,四边形BDCE为平行四边形.
解答 解:(1)相等.
理由:∵BE、BD分别是角平分线,
∴∠CBE=∠FBE,∠CBD=∠ABD,
∵l∥AB,
∴∠ABD=∠BDE=∠CBD,∠BED=∠FBE=∠CBE,
∴DO=OB,OB=OE,
∴DO=EO.
(2)∵BE、BD分别是角平分线,
∴∠CBE=$\frac{1}{2}$∠FBC,∠CBD=$\frac{1}{2}$∠ABC,
∴∠DBE=∠DBC+∠CBE=$\frac{1}{2}$(∠FBC+∠ABC)=$\frac{1}{2}×$180°=90°.
在RT△DBE中,∵BD=2,BE=5,
∴DE=$\sqrt{D{B}^{2}+B{E}^{2}}=\sqrt{{2}^{2}+{5}^{2}}=\sqrt{29}$,
∴OB=$\frac{1}{2}$DE=$\frac{\sqrt{29}}{2}$.
(3)当点O在BC中点时,四边形BDCE为矩形.
理由:由(1)知,OD=OE,当CO=BO时,四边形BDCE为平行四边形,
由(2)知,∠DBE=90°,所以四边形BDCE为矩形.
即当O为BC的中点时,四边形BDCE为矩形.
点评 本题是一道四边形只是的综合题,考察了平行线的性质、角平分线的性质、等腰三角形的判定、直角三角形斜边的中线与斜边的关系、勾股定理以及平行四边形、矩形的判定.利用“邻补角的角平分线所构成的角是直角”“直角三角形斜边的中线等于斜边的一半”是解决本题的关键.

 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案| A. | 10n | B. | $\frac{n}{10}$ | C. | 10m | D. | $\frac{m}{10}$ |
| 尺码(单位:cm) | 人数 |
| 140≤x<150 | 7 |
| 150≤x<160 | 30 |
| 160≤x<170 | 10 |
| 170≤x<180 | 3 |
| A. | -7 | B. | -6 | C. | -5 | D. | -4 |
| 进价(元/只) | 售价(元/只) | |
| 甲种节能灯 | 30 | 40 |
| 乙种节能灯 | 35 | 50 |
(2)全部售完100只节能灯后,该商场获利多少元?
 如图,AE∥BF,AC平分∠BAE,交BF于C.
如图,AE∥BF,AC平分∠BAE,交BF于C. 如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,且点C的横坐标是6,连接CA并延长交y轴于点P,连接BP,BC.则△PBC的面积是24.
如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,且点C的横坐标是6,连接CA并延长交y轴于点P,连接BP,BC.则△PBC的面积是24.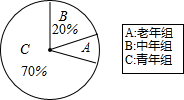 2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男运动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年组共有210人,则老年组共有30人.
2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男运动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年组共有210人,则老年组共有30人.