题目内容
19.某校七(7)班50名学生的校服尺码经统计如下:| 尺码(单位:cm) | 人数 |
| 140≤x<150 | 7 |
| 150≤x<160 | 30 |
| 160≤x<170 | 10 |
| 170≤x<180 | 3 |
分析 根据加权平均数的求解方法列式进行计算即可得解.
解答 解:$\frac{7}{50}$×145+$\frac{30}{50}$×155+$\frac{10}{50}$×165+$\frac{3}{50}$×175,
=$\frac{1}{50}$×(1015+4650+1650+525),
=$\frac{1}{50}$×7840,
=156.8,
答:这50名学生的校服尺码的平均数是156.8cm.
点评 本题考查的是加权平均数的求法,理解加权平均数的定义并准确计算是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.若a>1,则1+$\frac{\sqrt{(1-a)^{2}}}{a-1}$的值是( )
| A. | 1 | B. | 2 | C. | 0 | D. | -1 |
7.已知a和b是有理数,若a+b=0,ab≠0,则在a和b之间一定( )
| A. | 存在负整数 | B. | 存在正整数 | C. | 存在负分数 | D. | 不存在正分数 |
14.直线y=-$\frac{1}{2}$x+1和y=$\frac{1}{2}$x+1的交点坐标是( )
| A. | (0,1) | B. | (1,0) | C. | (1,$\frac{1}{2}$) | D. | (-1,$\frac{3}{2}$) |
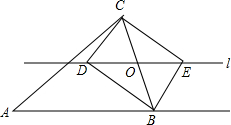 如图,∠CBF是△ABC的一个外角,点O是BC上的任意一点(不与B、C重合),过点O作直线l∥AB,且直线l与∠ABC的平分线相交于D,与∠CBF的平分线相交于E,
如图,∠CBF是△ABC的一个外角,点O是BC上的任意一点(不与B、C重合),过点O作直线l∥AB,且直线l与∠ABC的平分线相交于D,与∠CBF的平分线相交于E, 如图,正方形ABCD中,AD=8,E是对角线AC的中点,动点P从点A出发,沿AB方向以每秒1个单位的速度向终点B运动,同时动点Q从点B出发,以每秒2个单位的速度先沿BC方向运动到点C,再沿CD方向向终点D运动,连接EP,EQ,以EP、EQ为邻边作?PEQF,设点P运动的时间为t秒(t>0)
如图,正方形ABCD中,AD=8,E是对角线AC的中点,动点P从点A出发,沿AB方向以每秒1个单位的速度向终点B运动,同时动点Q从点B出发,以每秒2个单位的速度先沿BC方向运动到点C,再沿CD方向向终点D运动,连接EP,EQ,以EP、EQ为邻边作?PEQF,设点P运动的时间为t秒(t>0)