题目内容
20.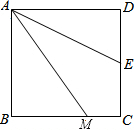 如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.(1)求证:AM=AD+MC;
(2)若AD=4,求AM的长.
分析 (1)从平行线和中点这两个条件出发,延长AE、BC交于点N,易证△ADE≌△NCE,从而有AD=CN,只需证明AM=NM即可.
(2)设MC=x,则BM=4-x,由勾股定理与(1)的结论得出AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{{4}^{2}+(4-x)^{2}}$=4+x,解得x即可得出结果.
解答 (1)证明:延长AE、BC交于点N,如图所示:
∵四边形ABCD是正方形,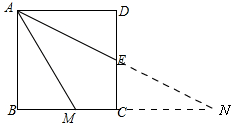
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAM,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
∴AM=MN,
在△ADE和△NCE中,$\left\{\begin{array}{l}{∠DAE=∠MAE}\\{∠AED=∠NEC}\\{DE=CE}\end{array}\right.$,
∴△ADE≌△NCE(AAS),
∴AD=NC,
∴AM=MN=NC+MC=AD+MC;
(2)解:∵四边形ABCD是正方形,
∴AB=BC=AD=4,∠B=90°,
设MC=x,则BM=4-x,
AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{{4}^{2}+(4-x)^{2}}$,
∵AM=AD+MC=4+x,
∴$\sqrt{{4}^{2}+(4-x)^{2}}$=4+x,
解得:x=1,
∴AM=5.
点评 本题主要考查了全等三角形的性质和判定、矩形的性质、角平分线的性质、勾股定理等知识,通过作辅助线构造全等三角形是解决问题的关键.

练习册系列答案
相关题目
10. 如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )
如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )
 如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )
如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )| A. | DE是△ABC的中位线 | B. | 点O是△ABC的重心 | ||
| C. | △DEO∽△CBO | D. | $\frac{{S}_{△DOE}}{{S}_{△ADE}}$=$\frac{1}{2}$ |
11. 六个大小相同的正方体搭成的几何体如图所示,其左视图是( )
六个大小相同的正方体搭成的几何体如图所示,其左视图是( )
 六个大小相同的正方体搭成的几何体如图所示,其左视图是( )
六个大小相同的正方体搭成的几何体如图所示,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
8.在我县中学生春季田径运动会上,参加男子跳高的16名运动员的成绩如下表所示:
这些运动员跳高成绩的中位数和众数分别是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 3 | 3 | 4 | 3 | 2 |
| A. | 1.70,1.65 | B. | 1.70,1.70 | C. | 1.65,1.70 | D. | 3,3 |


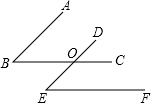 如图,已知AB∥DE,∠B=∠E,求证:BC∥EF.
如图,已知AB∥DE,∠B=∠E,求证:BC∥EF.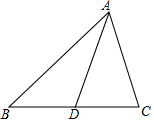 已知AD是△ABC的角平分线,求证:AB•AC=AD2+BD•CD.
已知AD是△ABC的角平分线,求证:AB•AC=AD2+BD•CD.