题目内容
11.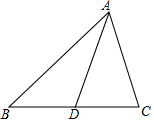 已知AD是△ABC的角平分线,求证:AB•AC=AD2+BD•CD.
已知AD是△ABC的角平分线,求证:AB•AC=AD2+BD•CD.
分析 作辅助圆,根据同弧所对的圆周角相等和角平分线证明相似得出比例式,再证△BAD∽△ECD,根据相似三角形的性质得出AD•ED=BD•DC,即可得出答案.
解答  证明:作△ABC的外接圆O,延长AD交⊙O于E,连接CE,
证明:作△ABC的外接圆O,延长AD交⊙O于E,连接CE,
∵AE平分∠BAC,
∴∠BAD=∠EAC,
∵∠B=∠E,
∴△ABD∽△AEC
∴$\frac{AB}{AE}=\frac{AD}{AC}$,
∴AB•AC=AD•AE=AD(AD+DE)=AD2+AD•ED,
∵∠B=∠E,∠BAD=∠DCE,
∴△BAD∽△ECD,
∴$\frac{AD}{CD}=\frac{BD}{ED}$,
∴AD•ED=BD•DC,
∴AB•AC=AD•AE=AD2+BD•DC.
点评 本题考查了相似三角形的性质和判定,圆周角定理的应用,解此题的关键是推出△ABD∽△AEC和△BAD∽△ECD,主要考查学生的推理能力.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
1.若分式$\frac{x+2}{x-1}$有意义,则x的取值范围是( )
| A. | x≥1 | B. | x≠1 | C. | x≥-2 | D. | x≠-2 |
18.下列根式中不是最简二次根式的是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{12}$ | C. | $\sqrt{14}$ | D. | $\frac{\sqrt{17}}{2}$ |
20.下列说法正确的是( )
| A. | 一个数的相反数一定是负数 | B. | 若|a|=|b|,则a=b | ||
| C. | 若|m|=2,则m=±2 | D. | -a一定是负数 |
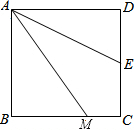 如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM. 如图,以等腰三角形ABC的底边BC为直径的圆O分别交两腰于D、E,连结DE,求证:
如图,以等腰三角形ABC的底边BC为直径的圆O分别交两腰于D、E,连结DE,求证: