题目内容
1.在△ABC中,∠B=90°,AD平分∠BAC交BC于D,DE是AC的垂直平分线,若BD=1,那么BC=3.分析 根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,角平分线上的点到角的两边的距离相等可得DC=DE,然后根据直角三角形的性质即可得到结论.
解答  解:∵∠B=90°,DE是AC的垂直平分线,若BD=1,
解:∵∠B=90°,DE是AC的垂直平分线,若BD=1,
∴DC=AD,BD=DE,CE=AE,
∵AD平分∠BAC交BC于D,
∴AB=AE,
∴AC=2AB,
∴∠C=30°∴∠CAB=60°,
∴∠BAD=30°,
∴AD=2BD=2,
∴CD=2,
∴BC=3.\
故答案为:3.
点评 本题考查了线段垂直平分线的性质,直角三角形的性质,熟练掌握线段垂直平分线的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.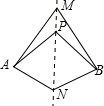 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )| A. | AM=BM | B. | ∠ANM=∠BNM | C. | ∠MAP=∠MBP | D. | AP=BN |
9.下列选项中,能使关于x的一元二次方程ax2-4x+c=0一定有实数根的是( )
| A. | a>0 | B. | a=0 | C. | c<0 | D. | c=0 |
16.在直角坐标系中,点A(-3,5)与点B关于x轴对称,则( )
| A. | B(3,5) | B. | B(-3,-5) | C. | B(5,3) | D. | B(5,-3) |
6. 如图,若OB平分∠AOC,OC平分∠BOD,且∠AOB=25°,则∠AOD等于( )
如图,若OB平分∠AOC,OC平分∠BOD,且∠AOB=25°,则∠AOD等于( )
 如图,若OB平分∠AOC,OC平分∠BOD,且∠AOB=25°,则∠AOD等于( )
如图,若OB平分∠AOC,OC平分∠BOD,且∠AOB=25°,则∠AOD等于( )| A. | 25° | B. | 50° | C. | 75° | D. | 90° |
13.16的平方根是( )
| A. | ±4 | B. | ±2 | C. | 4 | D. | 2 |
10.已知⊙O的半径为1,点A到圆心O的距离为a,若关于x的方程x2-2x+a=0不存在实数根,则点A与⊙O的位置关系是( )
| A. | 点A在⊙O外 | B. | 点A在⊙O上 | C. | 点A在⊙O内 | D. | 无法确定 |
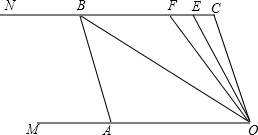 如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,点F在线段CB上,OB平分∠AOF,OE平分∠COF.
如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,点F在线段CB上,OB平分∠AOF,OE平分∠COF.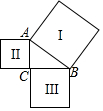 如图,以Rt△ABC的三边为边分别作正方形Ⅰ、Ⅱ、Ⅲ,已知正方形Ⅰ与正方形Ⅱ的面积分别为25和9,则正方形Ⅲ的面积为( )
如图,以Rt△ABC的三边为边分别作正方形Ⅰ、Ⅱ、Ⅲ,已知正方形Ⅰ与正方形Ⅱ的面积分别为25和9,则正方形Ⅲ的面积为( )