题目内容
11.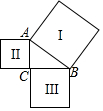 如图,以Rt△ABC的三边为边分别作正方形Ⅰ、Ⅱ、Ⅲ,已知正方形Ⅰ与正方形Ⅱ的面积分别为25和9,则正方形Ⅲ的面积为( )
如图,以Rt△ABC的三边为边分别作正方形Ⅰ、Ⅱ、Ⅲ,已知正方形Ⅰ与正方形Ⅱ的面积分别为25和9,则正方形Ⅲ的面积为( )| A. | 4 | B. | 8 | C. | 16 | D. | 34 |
分析 先设Rt△ABC的三边分别为a、b、c,再分别用a、b、c表示正方形Ⅲ的面积、正方形Ⅱ的面积、正方形Ⅰ的面积的值,由勾股定理即可得出正方形Ⅲ的面积的值.
解答 解:设Rt△ABC的三边分别为a、b、c,
∴正方形Ⅲ的面积=a2,正方形Ⅱ的面积=b2=9,正方形Ⅰ的面积=c2=25,
∵△ABC是直角三角形,
∴a2=b2+c2,
∴正方形Ⅲ的面积=25-9=16.
故选:C.
点评 本题考查的是勾股定理的应用及正方形的面积公式,熟知勾股定理是解答此题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
2.若x=3是方程a-x=7的解,则a的值是( )
| A. | 4 | B. | 10 | C. | 7 | D. | $\frac{7}{3}$ |
19.下列图案属于轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.下列实数中,不属于无理数的是( )
| A. | $\frac{22}{7}$ | B. | $\sqrt{3}$ | C. | 100π | D. | $\sqrt{\frac{1}{2}}$ |