题目内容
8.计算:(1)2(m+1)2-(2m+1)(2m-1);
(2)4x2-(-2x+3)(-2x-3);
(3)先化简,再求值:[(x+2y)2-(x+y)(3x-y)-5y2]÷2x,其中x=-2,y=$\frac{1}{2}$.
分析 (1)先根据完全平方公式和平方差公式算乘法,再合并同类项即可;
(2)先算平方差公式化简,再合并同类项即可;
(3)先算乘法,再合并同类项,算除法,最后代入求出即可.
解答 解:(1)原式=2(m2+2m+1)-(4m2-1)
=2m2+4m+2-4m2+1
=-2m2+4m+3;
(2)原式=4x2-(4x2-9)
=4x2-4x2+9
=9;
(3)[(x+2y)2-(x+y)(3x-y)-5y2]÷2x
=[x2+4xy+4y2-3x2+xy-3xy+y2-5y2]÷2x
=[-2x2+2xy]÷2x
=-x+y,
当x=-2,y=$\frac{1}{2}$时,原式=-(-2)+$\frac{1}{2}$=2$\frac{1}{2}$.
点评 本题考查了整式的混合运算和求值,能正确根据整式的运算法则进行化简是解此题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
19.据统计,2009年在国际金融危机的强烈冲击下,我国国内生产总值约为30 067 000 000 000元,仍比上年增长9.0%.30 067 000 000 000元用科学记数法表示为(保留三位有效数字)( )
| A. | 3.0037×1013元 | B. | 3.00×1013元 | C. | 30.1×1012元 | D. | 3.01×1013元 |
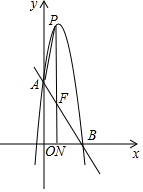 如图,直线y=-$\frac{3}{2}$x+3分别交y轴、x轴于点A,B,抛物线y=-4x2+bx+c经过点A,B,点P在该抛物线的图象上,作PN⊥x轴于点N,PN交射线AB于点F,连结AP,设点P横坐标为n(n>0).
如图,直线y=-$\frac{3}{2}$x+3分别交y轴、x轴于点A,B,抛物线y=-4x2+bx+c经过点A,B,点P在该抛物线的图象上,作PN⊥x轴于点N,PN交射线AB于点F,连结AP,设点P横坐标为n(n>0).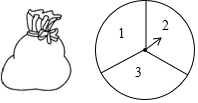 一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去,否则小亮去.
一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去,否则小亮去.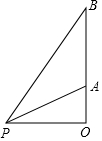 如图,一枚火箭从地面O处发射,在距离发射点9km处的地面观测站P点测得火箭底部到达A点时,其底部的仰角为30°;20s后火箭底部到达B点,测得其底部的仰角为60°.求这枚火箭从A点到B点的平均速度(精确到 0.1km/s)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24)
如图,一枚火箭从地面O处发射,在距离发射点9km处的地面观测站P点测得火箭底部到达A点时,其底部的仰角为30°;20s后火箭底部到达B点,测得其底部的仰角为60°.求这枚火箭从A点到B点的平均速度(精确到 0.1km/s)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24)