题目内容
1. 如图,在等腰△ABC中,AB=AC,过点B作DB⊥BC于点B,交过点A直线DE交于点D,且∠ADB=135°,AE=2AD,连接CE,若sin∠ABC=$\frac{{2\sqrt{5}}}{5}$,DB=1时,则CE=$\sqrt{17}$.
如图,在等腰△ABC中,AB=AC,过点B作DB⊥BC于点B,交过点A直线DE交于点D,且∠ADB=135°,AE=2AD,连接CE,若sin∠ABC=$\frac{{2\sqrt{5}}}{5}$,DB=1时,则CE=$\sqrt{17}$.
分析 作辅助线构建等腰直角三角形和直角三角形,分别得出△BDF和△AFM是等腰直角三角形,得BF=DB=1,AM=FM,根据sin∠ABC=$\frac{{2\sqrt{5}}}{5}$设未知数,表示BM和AM的长,列方程得出各线段的长,并证出AG是△EFC的中位线,由此得出结论.
解答 解: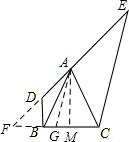 过A作AM⊥BC,垂足为M,延长AD、CB交于F,取FC的中点G,连接AG,
过A作AM⊥BC,垂足为M,延长AD、CB交于F,取FC的中点G,连接AG,
∵∠ADB=135°,
∴∠BDF=180°-135°=45°,
∴△BDF是等腰直角三角形,
∴BF=DB=1,
由勾股定理得:DF=$\sqrt{2}$,
在Rt△AFM中,∵∠F=45°,
∴AM=FM,
设AM=2$\sqrt{5}$x,AB=5x,则BM=$\sqrt{5}$x,
由AM=FM得:$\sqrt{5}$x+1=2$\sqrt{5}$x,
x=$\frac{\sqrt{5}}{5}$,
∴BM=MC=$\sqrt{5}$x=1,AM=2,
∵AM⊥BC,DB⊥BC,
∴DB∥AM,
∵FB=BM,
∴FD=AD,
∵AE=2AD,
∴AE=AF,
∴AG是△EFC的中位线,
∴EC=2AG,
∵MG=$\frac{1}{2}$,
由勾股定理得:AG=$\sqrt{{2}^{2}+(\frac{1}{2})^{2}}$=$\sqrt{\frac{17}{4}}$=$\frac{\sqrt{17}}{2}$,
∴EC=$\sqrt{17}$.
点评 本题主要考查了三角形中位线性质的运用,同时也考查了解直角三角形,如果题中已知某一角的三角函数值,而这个值不是特殊角,要根据这个数值的比的关系设未知数,表示出相关线段的长,但要注意利用这一数值表示边长时,必须在直角三角形中.

练习册系列答案
相关题目
2. 在诸城市开展的“大美龙城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如下:
在诸城市开展的“大美龙城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如下:
(1)统计表中的m=100,x=40,y=0.18;
(2)请将频数分布直方图补充完整;
(3)电视台要从参加义务劳动的学生中随机抽取1名同学采访,抽到是参加义务劳动的时间为2小时的同学概率是多少?
 在诸城市开展的“大美龙城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如下:
在诸城市开展的“大美龙城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如下:| 劳动时间(时) | 频数(人数) | 频率 |
| 0.5 | 12 | 0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合计 | m | 1 |
(2)请将频数分布直方图补充完整;
(3)电视台要从参加义务劳动的学生中随机抽取1名同学采访,抽到是参加义务劳动的时间为2小时的同学概率是多少?

 学校计划利用一块空地修建一个学生自行车棚,其中一面靠墙,这堵墙的长度为12米,建造车棚的面积为80平方米.已知新建板墙的木板材料的总长为26米.为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么车棚的长与宽分别为多少米?
学校计划利用一块空地修建一个学生自行车棚,其中一面靠墙,这堵墙的长度为12米,建造车棚的面积为80平方米.已知新建板墙的木板材料的总长为26米.为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么车棚的长与宽分别为多少米? 如图,有一圆形展厅,在其圆形边缘上的点A处安装了一台监视器,它的监控角度是70°,为了监控整个展厅,最少需在圆形的边缘上共安装这样的监视器( )
如图,有一圆形展厅,在其圆形边缘上的点A处安装了一台监视器,它的监控角度是70°,为了监控整个展厅,最少需在圆形的边缘上共安装这样的监视器( )