题目内容
10．解方程组：$\left\{\begin{array}{l}{8359x+1641y=28359}\\{1641x+8359y=21641}\end{array}\right.$．分析 方程组两方程相加求出x+y的值，利用加减消元法求出解即可．
解答 解：$\left\{\begin{array}{l}{8359x+1641y=28359①}\\{1641x+8359y=21641②}\end{array}\right.$，
①+②得：10000（x+y）=50000，即x+y=5③，
①-③×1641得：6718x=20154，即x=3，
把x=3代入③得：y=2，
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
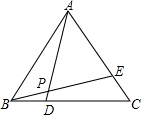如图，在等边△ABC中，D、E分别在BC、AC上，BD=CE，AD与BE交于点P．
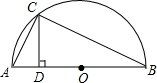如图所示，AB是半圆O的直径，CD⊥AB，AC=5cm，BC=12cm，求CD的长．
2．二次函数y=a（x+k）2+k，无论k为何实数，其图象的顶点都在（ ）
| A． | 直线y=x上 | B． | 直线y=-x上 | C． | x轴上 | D． | y轴上 |