题目内容
5.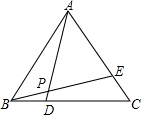 如图,在等边△ABC中,D、E分别在BC、AC上,BD=CE,AD与BE交于点P.
如图,在等边△ABC中,D、E分别在BC、AC上,BD=CE,AD与BE交于点P.(1)求证:△ABD≌△BCE;
(2)求∠APE的度数.
分析 (1)因为△ABC为等边三角形,所以∠ABD=∠BCE=60°,AB=AC=BC,又BD=CE,所以用“SAS”可判定△ABD≌△BCE;
(2)根据全等三角形的性质得出∠BAD=∠CBE,利用三角形外角性质解答即可.
解答 (1)证明:∵△ABC为等边三角形,
∴AB=AC=BC,∠ABD=∠BCE=60°,
在△ABD和△BCE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠BCE=60°}\\{BD=CE(已知)}\end{array}\right.$,
∴△ABD≌△BCE(SAS);
(2)∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∵∠ADC=∠CBE+∠BPD=∠BAD+∠B,
∴∠BPD=∠B=∠APE=60°.
点评 本题考查了全等三角形的判定和性质,关键是根据等边三角形的性质:等边三角形的三个内角都相等,且都等于60°;三条边相等.

练习册系列答案
相关题目
13.在平面直角坐标系中,点P(2,-1)关于y轴对称的点Q的坐标为( )
| A. | (-2,-1) | B. | (-2,1) | C. | (2,1) | D. | (1,-2) |
 如图,直线y=-3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=$\frac{k}{x}$(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=$\frac{k}{x}$(k≠0)上的点D1处,则a=2.
如图,直线y=-3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=$\frac{k}{x}$(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=$\frac{k}{x}$(k≠0)上的点D1处,则a=2. 如图,在四边形ABCO中,点A与点C关于x轴对称,点B的坐标为(2,0),点C的坐标为(1,2),求点A的坐标及对角线OB,AC的长.
如图,在四边形ABCO中,点A与点C关于x轴对称,点B的坐标为(2,0),点C的坐标为(1,2),求点A的坐标及对角线OB,AC的长.