题目内容
10.为测山高,在点A处测得山顶D的仰角为31°,从点A向山方向前进140米到达点B,在B处测得山顶D的仰角为62°(如图).(1)在所给的图②中尺规作图:过点D作DC⊥AB,交AB的延长线于点C;
(2)山高DC是多少(结果取整数)?

分析 (1)以D为圆心,大于DC长度为半径作弧,与AB及其延长线相交于E、F,分别以E、F为圆心,ED为半径作弧,相交于G,过D、G作垂线即可;
(2)根据角的度数判断出AB=DB,利用三角函数求出DC即可.
解答  解:(1)如图②,
解:(1)如图②,
(2)如图②,
∵∠DBC=62°,∠DAB=31°,
∴∠BDA=∠DAB=31°,
∴AB=DB,
∵AB=140米,
∴DB=140米,
在Rt△DCB中,∠C=90°,sin∠DBC=$\frac{DC}{DB}$,
∴DC=140•sin62°≈124米.
答:山高124米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,将实际问题转化到三角形中是解题的关键.

练习册系列答案
相关题目
20.下列计算正确的是( )
| A. | (ab)2=a2b2 | B. | (a+b)2=a2+b2 | C. | (a4)2=a6 | D. | a6÷a2=a3 |
18.一元二次方程x2-4x-m=0总有实数根,则m应满足的条件是( )
| A. | m>-4 | B. | m=-4 | C. | m≤-4 | D. | m≥-4 |
5. 如图,如果∠1+∠2=180°,那么( )
如图,如果∠1+∠2=180°,那么( )
 如图,如果∠1+∠2=180°,那么( )
如图,如果∠1+∠2=180°,那么( )| A. | ∠2+∠4=180° | B. | ∠3+∠4=180° | C. | ∠1+∠3=180° | D. | ∠1=∠4 |
15.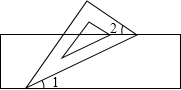 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )
如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )
 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )
如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )| A. | 23° | B. | 27° | C. | 30° | D. | 37° |
20. 如图,要使平行四边形ABCD变为矩形,需要添加的条件是( )
如图,要使平行四边形ABCD变为矩形,需要添加的条件是( )
 如图,要使平行四边形ABCD变为矩形,需要添加的条件是( )
如图,要使平行四边形ABCD变为矩形,需要添加的条件是( )| A. | AC=BD | B. | AD=BC | C. | AB=CD | D. | AB=BC |