题目内容
18.一元二次方程x2-4x-m=0总有实数根,则m应满足的条件是( )| A. | m>-4 | B. | m=-4 | C. | m≤-4 | D. | m≥-4 |
分析 由题意得到△≥0,然后解这个不等式即可得到答案.
解答 解:∵一元二次方程x2-4x-m=0总有实数根,
∴△≥0,
∴16-4(-m)=16+4m≥0,即m≥-4,
故选:D.
点评 本题主要考查了利用一元二次方程根的判别式(△=b2-4ac)判断方程的根的情况.
一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
8.下列运算中正确的是( )
| A. | 2a3•a4=2a7 | B. | 2(a+1)=2a+1 | C. | (2a4)3=8a7 | D. | a8÷a2=a4 |
6.把人民币大约943千万元用科学记数法表示为( )元.
| A. | 9.43×102 | B. | 0.943×103 | C. | 9.43×109 | D. | 9.43×1010 |
13.在有理数-3,0,3,4中,最小的有理数是( )
| A. | -3 | B. | 0 | C. | 3 | D. | 4 |
3.|-$\frac{1}{2}$|的相反数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |

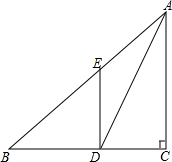 如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,点E在AB上,DE∥AC,CD=12,BD=15,求AE、BE的长.
如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,点E在AB上,DE∥AC,CD=12,BD=15,求AE、BE的长.