题目内容
18.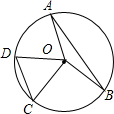 如图,半径为5的⊙O中,弦AB,CD所对的圆心角分别是∠AOB,∠COD.已知AB=8,∠AOB+∠COD=180°,则弦CD的弦心距等于( )
如图,半径为5的⊙O中,弦AB,CD所对的圆心角分别是∠AOB,∠COD.已知AB=8,∠AOB+∠COD=180°,则弦CD的弦心距等于( )| A. | $\frac{5}{2}$ | B. | 3 | C. | $\frac{7}{2}$ | D. | 4 |
分析 作OF⊥DC于F,作直径DE,连接CE,先由∠AOB+∠COD=180°,及∠COE+∠COD=180°,利用等角的补角相等得到:∠AOB=∠COE,进而由在同圆中,相等的圆心角所对的弧相等得到:$\widehat{AB}=\widehat{CE}$,然后由等弧所对的弦相等可得:CE=AB=8,然后由OF⊥DC,根据垂径定理得DF=CF,然后由OD=OE,可得OF为△DCE的中位线,然后根据三角形中位线性质得到:OF=$\frac{1}{2}$CE=4,即得到弦CD的弦心距.
解答 解:作OF⊥DC于F,作直径DE,连接CE,如图,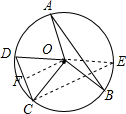
∵∠AOB+∠COD=180°,
而∠COE+∠COD=180°,
∴∠AOB=∠COE,
∴$\widehat{AB}=\widehat{CE}$,
∴CE=AB=8,
∵OF⊥CD,
∴DF=CF,
而OD=OE,
∴OF为△DCE的中位线,
∴OF=$\frac{1}{2}$CE=4.
故选:D.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理和三角形中位线性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.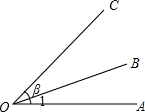 如图,下列表示角的说法,错误的是( )
如图,下列表示角的说法,错误的是( )
 如图,下列表示角的说法,错误的是( )
如图,下列表示角的说法,错误的是( )| A. | ∠AOC也可用∠O表示 | B. | ∠1与∠AOB表示同一个角 | ||
| C. | ∠β表示的是∠BOC | D. | ∠AOB和∠BOC都不能用∠O表示 |
5.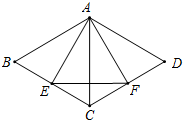 如图,已知等边三角形AEF的两个顶点E、F都在菱形ABCD的边上,EF⊥AC,下列结论,①CE=CF;②∠BAE=∠DAF;③BE=EC;④三角形AEF的面积等于菱形ABCD的面积的一半,其中正确的个数是( )
如图,已知等边三角形AEF的两个顶点E、F都在菱形ABCD的边上,EF⊥AC,下列结论,①CE=CF;②∠BAE=∠DAF;③BE=EC;④三角形AEF的面积等于菱形ABCD的面积的一半,其中正确的个数是( )
 如图,已知等边三角形AEF的两个顶点E、F都在菱形ABCD的边上,EF⊥AC,下列结论,①CE=CF;②∠BAE=∠DAF;③BE=EC;④三角形AEF的面积等于菱形ABCD的面积的一半,其中正确的个数是( )
如图,已知等边三角形AEF的两个顶点E、F都在菱形ABCD的边上,EF⊥AC,下列结论,①CE=CF;②∠BAE=∠DAF;③BE=EC;④三角形AEF的面积等于菱形ABCD的面积的一半,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.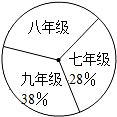 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )| 图书种类 | 频数 | 频率 |
| 科普知识 | 840 | B |
| 名人传记 | 816 | 0.34 |
| 漫画丛书 | A | 0.25 |
| 其它 | 144 | 0.06 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
3.抛物线y=x2-2x与坐标轴的交点个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
10.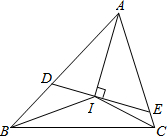 我们知道,任何一个三角形的三条内角平分线相交于一点.如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点.如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
(1)请你通过计算,填写表格.
(2)从表中你发现了∠BIC与∠BDI之间有何数量关系,请写出来,并说明其中的道理,它们的关系是∠BIC=∠BDI.
 我们知道,任何一个三角形的三条内角平分线相交于一点.如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点.如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.(1)请你通过计算,填写表格.
(2)从表中你发现了∠BIC与∠BDI之间有何数量关系,请写出来,并说明其中的道理,它们的关系是∠BIC=∠BDI.
| ∠BAC的度数 | 60° | 100° |
| ∠BIC的度数 | 120° | 140° |
| ∠BDI的度数 | 120° | 140° |
7.下列各数中,绝对值最小的数是( )
| A. | -1 | B. | π-3 | C. | 0.3 | D. | -$\sqrt{1.2}$ |