题目内容
7．下列各数中，绝对值最小的数是（ ）| A． | -1 | B． | π-3 | C． | 0.3 | D． | -$\sqrt{1.2}$ |
分析 根据绝对值的意义，计算出各选项的绝对值，然后再比较大小即可．
解答 解：∵|-1|=1，|π-3|≈0.14，|0.3|=0.3，|-$\sqrt{1.2}$|≈1.1，
∴绝对值最小的数是π-3．
故选B．
点评 本题考查的是实数的大小比较，熟知绝对值的性质是解答此题的关键．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
18．
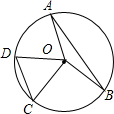如图，半径为5的⊙O中，弦AB，CD所对的圆心角分别是∠AOB，∠COD．已知AB=8，∠AOB+∠COD=180°，则弦CD的弦心距等于（ ）
如图，半径为5的⊙O中，弦AB，CD所对的圆心角分别是∠AOB，∠COD．已知AB=8，∠AOB+∠COD=180°，则弦CD的弦心距等于（ ）| A． | $\frac{5}{2}$ | B． | 3 | C． | $\frac{7}{2}$ | D． | 4 |
15．
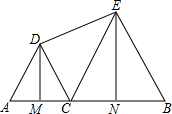如图，AB=2a，点C是线段AB上的一个动点，△ACD和△BCE是在AB同侧的两个等边三角形，DM，EN分别是△ACD和△BCE的高，点C在线段AB上沿着点A向点B的方向移动（不与点A、B重合），连接DE，得到四边形DMNE．这个四边形的面积为（ ）
如图，AB=2a，点C是线段AB上的一个动点，△ACD和△BCE是在AB同侧的两个等边三角形，DM，EN分别是△ACD和△BCE的高，点C在线段AB上沿着点A向点B的方向移动（不与点A、B重合），连接DE，得到四边形DMNE．这个四边形的面积为（ ）| A． | a2 | B． | $\frac{\sqrt{3}}{2}$a2 | C． | $\frac{\sqrt{3}}{4}$a2 | D． | 不能确定 |
2．如图，在圆形纸片和三角形纸片中都刚好能裁剪出棱长为acm的正方体纸盒的表面，那么两种纸片的利用率（纸片利用率=$\frac{纸片被利用的面积}{纸片的总面积}$×100%）的大小关系为（ ）
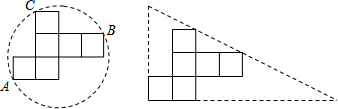
| A． | 圆形纸片利用率大 | B． | 三角形纸片利用率大 | ||
| C． | 两种纸片的利用率一样 | D． | 利用率与a的值有关，无法判断 |
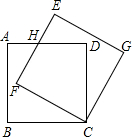如图所示，边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG，
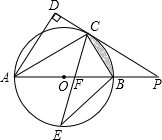如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为D，直线DC与AB的延长线交于点P，弦CE平分∠ACB，交AB于点F，连结BE，BE=7$\sqrt{2}$．下列四个结论：①AC平分∠DAB；②PF2=PB•PA；③若BC=$\frac{1}{2}$OP，则阴影部分的面积为$\frac{7}{4}$π-$\frac{49}{4}$$\sqrt{3}$；④若PC=24，则tan∠PCB=$\frac{3}{4}$．其中正确的是（ ）