题目内容
1.如图,抛物线y=$\frac{1}{4}$x(x-k)经过原点O,交x轴正半轴于A,过A的直线交抛物线于另一点B,AB交y轴正半轴于C,且OC=OA,B点的纵坐标为9(1)求抛物线的解析式;
(2)点P为第一象限的抛物线上一点,连接PB、PC,设P点的横坐标为m,△PBC的面积为S,求S与m的函数关系式;
(3)在(2)的条件下,连接OP、AP,若∠APO=45°,求点P的坐标.
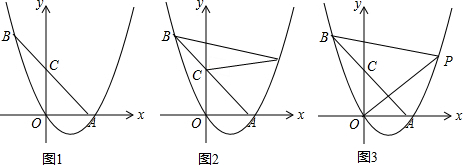
分析 (1)如图1中,作BH⊥x轴于H.由题意OC=OA=K,∠AOC=90°,推出∠OAC=∠OCA=45°,由∠BHA=90°,推出∠HBA=∠HAB=45°,推出BH=AH=9,推出OH=9-k,推出B(k-9,9),把B(k-9,9)代入y=$\frac{1}{4}$x(x-k),解方程即可.
(2)如图2中,作BH⊥x轴于H,连接OP、PH、PA.设P[m,$\frac{1}{4}$m(m-5)].根据S△PBC=S△PAB-S△PCA=(S△PBH+S△PHA-S△ABH)-(S△PCO+S△POA-S△AOC)计算即可.
(3)如图3中设AC交OP于D,AC的中点为K,连接PK.只要证明∠CPA=90°,根据PK=$\frac{5\sqrt{2}}{2}$,利用两点间距离公式,列出方程,解方程即可解决问题.
解答 解:(1)如图1中,作BH⊥x轴于H.
由题意OC=OA=K,∠AOC=90°,
∴∠OAC=∠OCA=45°,
∵∠BHA=90°,
∴∠HBA=∠HAB=45°,
∴BH=AH=9,
∴OH=9-k,
∴B(k-9,9),
把B(k-9,9)代入y=$\frac{1}{4}$x(x-k),
得到9=$\frac{1}{4}$(k-9)×(-9),
∴k=5,
∴抛物线的解析式为y=$\frac{1}{4}$x(x-5).
(2)如图2中,作BH⊥x轴于H,连接OP、PH、PA.设P[m,$\frac{1}{4}$m(m-5)].
∵P(-4,9),A(5,0),C(0,5),
∴S△PBC=S△PAB-S△PCA=(S△PBH+S△PHA-S△ABH)-(S△PCO+S△POA-S△AOC)
=$\frac{1}{2}$×9×(m+4)+$\frac{1}{2}$×9×$\frac{1}{4}$m(m-5)-$\frac{1}{2}$×9×9-[$\frac{1}{2}$×5×m+$\frac{1}{2}$×5×$\frac{1}{4}$m(m-5)-$\frac{1}{2}$×5×5]
=$\frac{1}{2}$m2-m-10(m>5).
(3)如图3中设AC交OP于D,AC的中点为K,连接PK.
∵∠DPA=∠DCO=45°,∠PDA=CDO,
∴△PDA∽△CDO,
∴$\frac{PD}{CD}$=$\frac{AD}{OD}$,
∴$\frac{PD}{AD}$=$\frac{CD}{OD}$,∵∠CDP=∠ODP,
∴△CDP∽△ODA,
∴∠CPD=∠OAD=45°,
∴∠CPA=90°,
∵CK=KA,
∴PK=$\frac{1}{2}$AC=$\frac{5\sqrt{2}}{2}$,
设P[m,$\frac{1}{4}$m(m-5)],
∵K($\frac{5}{2}$,$\frac{5}{2}$),
∴(m-$\frac{5}{2}$)2+[$\frac{1}{4}$m(m-5)-$\frac{5}{2}$]2=($\frac{5\sqrt{2}}{2}$)2,
整理得m(m-5)(m2-5m-4)=0,
∴m=0或5或$\frac{5+\sqrt{41}}{2}$或$\frac{5-\sqrt{41}}{2}$,
∵m>5,
∴m=$\frac{5+\sqrt{41}}{2}$,
∴P($\frac{5+\sqrt{41}}{2}$,1).
点评 本题考查二次函数综合题、待定系数法、三角形的面积、相似三角形的判定和性质、两点间距离公式、勾股定理等知识,解题的关键是灵活应用所学知识解决问题,学会用分割法求三角形的面积,学会利用参数构建方程解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | 都是普查 | B. | 都是抽查 | C. | ①是普查②是抽查 | D. | ①是抽查②是普查 |
| A. | $\frac{2}{3}$=$\frac{2a}{3a}$ | B. | $\frac{3a}{3b}$=$\frac{a}{b}$ | C. | $\frac{a}{b}$=$\frac{a+1}{b+1}$ | D. | $\frac{a}{b}$=$\frac{{a}^{2}}{{b}^{2}}$ |
| A. | 8 | B. | 15 | C. | 30 | D. | 31 |
| A. | 2 | B. | -3 | C. | 3 | D. | 以上都不对 |

 如图,矩形ABCD中,点E、F分别在AB、CD上,BF∥DE,若AD=12cm,AB=7cm,且AE:EB=5:2,阴影部分面积为24cm2.
如图,矩形ABCD中,点E、F分别在AB、CD上,BF∥DE,若AD=12cm,AB=7cm,且AE:EB=5:2,阴影部分面积为24cm2.