题目内容
9.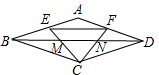 如图,在菱形ABCD中,点E、F分别是边AB、AD的中点,连接CE、CF交对角线BD于点M、N,连接EF,则BN:EF等于( )
如图,在菱形ABCD中,点E、F分别是边AB、AD的中点,连接CE、CF交对角线BD于点M、N,连接EF,则BN:EF等于( )| A. | 1:1 | B. | 1:2 | C. | 2:3 | D. | 3:2 |
分析 根据菱形的性质得出AB=AD=BC=CD,AD∥BC,AB∥CD,根据三角形的中位线性质得出BD=2EF,求出DC=2BE,B=2DF,根据相似三角形的判定得出△DFN∽△BCN,△BEM∽△DCM,求出$\frac{BE}{CD}$=$\frac{BM}{DM}$=$\frac{1}{2}$,$\frac{DF}{BC}$=$\frac{DN}{BC}$=$\frac{1}{2}$,求出BN=2BM,EF=3BM,即可得出答案.
解答 解:∵四边形ABCD是菱形,
∴AB=AD=BC=CD,AD∥BC,AB∥CD,
∵点E、F分别是边AB、AD的中点,
∴DC=2BE,BC=2DF,
∵AD∥BC,AB∥CD,
∴△DFN∽△BCN,△BEM∽△DCM,
∴$\frac{BE}{CD}$=$\frac{BM}{DM}$=$\frac{1}{2}$,$\frac{DF}{BC}$=$\frac{DN}{BC}$=$\frac{1}{2}$,
∴BM=MN,DN=MN,
∴BM=MN=DN,
∴BN=2BM,
∵点E、F分别是边AB、AD的中点,
∴BD=2EF=6BM,
∴EF=3BM,
∴BN:EF=2BM:3BM=2:3,
故选C.
点评 本题考查了菱形的性质和相似三角形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:菱形的对边平行,菱形的四条边都相等.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
17. 如图,AB为⊙O的直径,点C在⊙O上,连接AC,OC,过点B作BD⊥OC,交⊙O于点D,已知∠ACO=35°,则∠COD的度数为( )
如图,AB为⊙O的直径,点C在⊙O上,连接AC,OC,过点B作BD⊥OC,交⊙O于点D,已知∠ACO=35°,则∠COD的度数为( )
 如图,AB为⊙O的直径,点C在⊙O上,连接AC,OC,过点B作BD⊥OC,交⊙O于点D,已知∠ACO=35°,则∠COD的度数为( )
如图,AB为⊙O的直径,点C在⊙O上,连接AC,OC,过点B作BD⊥OC,交⊙O于点D,已知∠ACO=35°,则∠COD的度数为( )| A. | 70° | B. | 60° | C. | 45° | D. | 35° |
4. 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )| A. | (-2,2) | B. | (4,1) | C. | (3,1) | D. | (4,0) |
18.为纪念中国人民抗战战争的胜利,9月3日被确定为抗日战争胜利纪念日,某校为了了解学生对“抗日战争”的知晓情况,从全校6000名学生中,随机抽取了120名学生进行调查,在这次调查中( )
| A. | 6000名学生是总体 | |
| B. | 所抽取的每1名学生对“抗日战争”的知晓情况是总体的一个样本 | |
| C. | 120名是样本容量 | |
| D. | 所抽取的120名学生对“抗日战争”的知晓情况是总体的一个样本 |
 如图,是把圆柱体沿上面的直径截去一部分后剩下的物体图形,它的俯视图是( )
如图,是把圆柱体沿上面的直径截去一部分后剩下的物体图形,它的俯视图是( )



 如图是每个面上都有一个汉字的正方体的表面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的表面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )
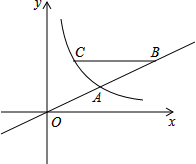 如图,在直角坐标系xOy中,反比例函数图象与直线y=$\frac{1}{2}$x相交于横坐标为2的点A.
如图,在直角坐标系xOy中,反比例函数图象与直线y=$\frac{1}{2}$x相交于横坐标为2的点A.