题目内容
16.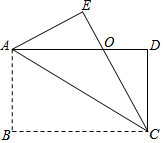 如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.(1)求证:EO=DO;
(2)若∠OCD=30°,AB=$\sqrt{3}$,求△ACO的面积.
分析 (1)根据翻折的性质和矩形的性质可得AE=CD,∠E=∠D=90°,再根据对顶角相等可得∠EOA=∠DOC,然后利用“角角边”证明△AEO和△CDO全等,根据全等三角形对应边相等证明即可;
(2)根据含30°角的直角三角形的特点求出OD、OC,再求出OA=OC,然后利用三角形的面积公式列式计算即可得解.
解答 (1)证明:由题可得:AE=CD,∠E=∠D=90°,
又∵∠EOA=∠DOC(对顶角相等),
∴△AEO≌△CDO(AAS),
∴EO=DO;
(2)解:∵AB=$\sqrt{3}$,
∴CD=$\sqrt{3}$,
∵∠OCD=30°,
∴OD=1,OC=2,
∵EC=AD,EO=DO,
∴OA=OC=2,
∴S△ACO=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$.
点评 本题考查了翻折变换的性质,全等三角形的判定与性质,翻折前后对应边相等,对应角相等,难点在于(2)熟悉含30°角的直角三角形的特点并求出相应的边的长度.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
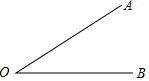 已知:∠AOB,如图,利用尺规作∠CDE,使∠CDE=∠AOB.
已知:∠AOB,如图,利用尺规作∠CDE,使∠CDE=∠AOB.