题目内容
15.己知一次函数y=kx-5和y=k′x+3,假设k>0,k′<0,则这两个一次函数图象的交点在第一或四象限.分析 根据一次函数的解析式画出函数图象,根据一次函数图象与系数的关系结合图形即可得出结论.
解答 解:分别作出一次函数y=kx-5和y=k′x+3的图象,如图所示.
∵在一次函数y=kx-5中,k>0,-5<0,
∴该一次函数图象过第一、三、四象限;
∵在一次函数y=k′x+3中,k′<0,3>0,
∴该一次函数图象过第一、二、四象限.
∴这两个一次函数图象的交点可能在第一或第四象限.
故答案为:一或四.
点评 本题考查了两条直线相交或平行问题以及一次函数图象与系数的关系,根据一次函数图象与系数的关系画出函数图象是解题的关键.

练习册系列答案
相关题目
10.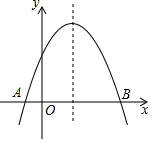 函数y=-x2+2(m-1)x+m+1的图象如图,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为( )
函数y=-x2+2(m-1)x+m+1的图象如图,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为( )
 函数y=-x2+2(m-1)x+m+1的图象如图,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为( )
函数y=-x2+2(m-1)x+m+1的图象如图,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为( )| A. | $\frac{1}{3}$或2 | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
7.某饭店所有员工的月收入情况如下:
该饭店所有员工月收入的众数是3000元.
| 经理 | 领班 | 迎宾 | 厨师 | 厨师助理 | 服务员 | |
| 人数(人) | 1 | 2 | 2 | 2 | 3 | 8 |
| 月收入(元) | 6700 | 3900 | 2800 | 4200 | 3200 | 3000 |
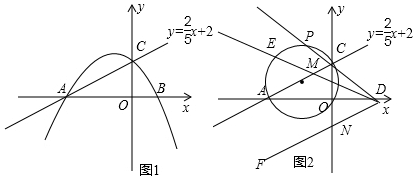
 如图所示,二次函数y=ax2+bx+c(a≠0)的图象与x轴相交于点A,B,若其对称轴为直线x=2,则OB-OA的值为4.
如图所示,二次函数y=ax2+bx+c(a≠0)的图象与x轴相交于点A,B,若其对称轴为直线x=2,则OB-OA的值为4.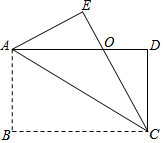 如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.