题目内容
18.先化简,再求值:$\frac{b}{{a}^{2}-{b}^{2}}$÷(1-$\frac{a}{a-b}$),其中a、b是2x2-2x-7=0的根.分析 先根据分式混合运算的法则把原式进行化简,再求出a+b的值代入进行计算即可.
解答 解:原式=$\frac{b}{(a+b)(a-b)}$÷$\frac{-b}{a-b}$
=$\frac{b}{(a+b)(a-b)}$•$\frac{a-b}{-b}$
=-$\frac{1}{a+b}$,
∵其中a、b是2x2-2x-7=0的根,
∴a+b=1,
∴原式=-1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.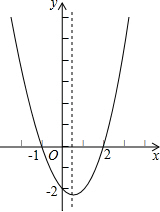 如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )
如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )
 如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )
如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )| A. | a>0,b<0,c>0 | B. | b2-4ac<0 | ||
| C. | 当-1<x<2时,y>0 | D. | 当x<$\frac{1}{2}$时,y随x的增大而减小 |
3.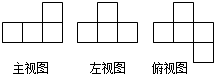 如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )
如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )
 如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )
如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
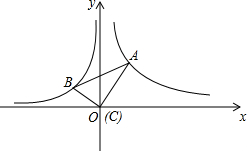 如图,在Rt△ABC中,∠A=30°,将△ABC放在平面直角坐标系中,使得直角顶点C与坐标原点O重合,此时顶点A恰好在双曲线y=$\frac{3}{x}$(x>0)上,顶点B恰好在双曲线y=$\frac{k}{x}$(x<0)上,则k的值为1.
如图,在Rt△ABC中,∠A=30°,将△ABC放在平面直角坐标系中,使得直角顶点C与坐标原点O重合,此时顶点A恰好在双曲线y=$\frac{3}{x}$(x>0)上,顶点B恰好在双曲线y=$\frac{k}{x}$(x<0)上,则k的值为1.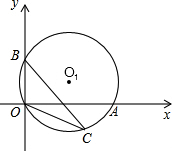 如图,在平面直角坐标系中,过点O的⊙O1与两坐标轴分别交于A、B两点A(4,0),B(0,2),点C在弧OA上,则tan∠BCO为$\frac{1}{2}$.
如图,在平面直角坐标系中,过点O的⊙O1与两坐标轴分别交于A、B两点A(4,0),B(0,2),点C在弧OA上,则tan∠BCO为$\frac{1}{2}$.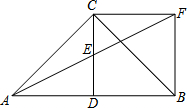 如图,在△ABC中,AC=BC,AC⊥BC,D是AB的中点,E是CD的中点,过点C作CF∥AB交AE的延长线于点F,连结BF.试判断四边形BDCF的形状,并证明你的结论.
如图,在△ABC中,AC=BC,AC⊥BC,D是AB的中点,E是CD的中点,过点C作CF∥AB交AE的延长线于点F,连结BF.试判断四边形BDCF的形状,并证明你的结论.