题目内容
 如图,直线OC,BC的函数关系式分别是y1=x和y2=-x+6,两直线的交点为C.
如图,直线OC,BC的函数关系式分别是y1=x和y2=-x+6,两直线的交点为C.(1)点C的坐标是(
(2)△COB是
(3)在直线y1找点D,使△DOB的面积是△COB的一半,求点D的坐标.
(4)作直线a⊥x轴,并交直线y1于点E,直线y2于点F,若EF的长度不超过3,求x的取值范围.
考点:一次函数综合题
专题:综合题
分析:(1)联立两直线解析式求出x与y的值,即为C坐标,根据C坐标,利用函数图象找出y1>y2时x的范围即可;
(2)△COB为等腰直角三角形,理由为:过C作CM垂直于x轴,根据C坐标确定出CM与OM的长,进而求出MB的长,分别利用勾股定理求出OC与BC的长,再利用勾股定理的逆定理得到三角形OBC为直角三角形,根据OC=BC即可得证;
(3)如图所示,分两种情况考虑,当D1为OC中点时;当O为D1D2中点时,分别根据△DOB的面积是△COB的一半,利用中点坐标公式求出D坐标即可;
(4)如图所示,分两种情况考虑:当直线a在C左侧时;当直线a在C右侧时,表示出EF的长,根据EF的长不超过3列出不等式,求出不等式的解集即可确定出x的范围.
(2)△COB为等腰直角三角形,理由为:过C作CM垂直于x轴,根据C坐标确定出CM与OM的长,进而求出MB的长,分别利用勾股定理求出OC与BC的长,再利用勾股定理的逆定理得到三角形OBC为直角三角形,根据OC=BC即可得证;
(3)如图所示,分两种情况考虑,当D1为OC中点时;当O为D1D2中点时,分别根据△DOB的面积是△COB的一半,利用中点坐标公式求出D坐标即可;
(4)如图所示,分两种情况考虑:当直线a在C左侧时;当直线a在C右侧时,表示出EF的长,根据EF的长不超过3列出不等式,求出不等式的解集即可确定出x的范围.
解答: 解:(1)联立得:
解:(1)联立得:
,
解得:x=3,y=3,
∴C(3,3),
根据图形得:当x>3时,y1>y2;
故答案为:3;3;>3;
(2)△COB为等腰直角三角形,理由为:
过C作CM⊥x轴,由C(3,3),得到CM=OM=3,
根据勾股定理得:OC=
=3
,
∵OB=6,OM=3,
∴BM=OB-OM=6-3=3,即CM=BM=3,
根据勾股定理得:BC=
=3
,
在△BCO中,OC=BC=3
,OB=6,
∵OC2+BC2=18+18=36,OB2=36,
∴OC2+BC2=OB2,
则△OBC为等腰直角三角形;
故答案为:等腰直角;
(3)如图所示,分两种情况考虑:
当D1为OC中点时,△D1OB的面积是△COB的一半,此时D1(
,
);
当O为D1D2中点时,△DOB的面积是△COB的一半,此时D2(-
,-
),
综上,D的坐标为(
,
)或(-
,-
);
(4)分两种情况考虑:
当直线a在C左侧时,此时EF=-x+6-x≤3,
解得:x≥
;
当直线a在C右侧时,此时EF=x-(-x+6)≤3,
解得:x≤
,
则x的范围为
≤x≤
.
 解:(1)联立得:
解:(1)联立得:
|
解得:x=3,y=3,
∴C(3,3),
根据图形得:当x>3时,y1>y2;
故答案为:3;3;>3;
(2)△COB为等腰直角三角形,理由为:
过C作CM⊥x轴,由C(3,3),得到CM=OM=3,
根据勾股定理得:OC=
| 32+32 |
| 2 |
∵OB=6,OM=3,
∴BM=OB-OM=6-3=3,即CM=BM=3,
根据勾股定理得:BC=
| 32+32 |
| 2 |
在△BCO中,OC=BC=3
| 2 |
∵OC2+BC2=18+18=36,OB2=36,
∴OC2+BC2=OB2,
则△OBC为等腰直角三角形;
故答案为:等腰直角;
(3)如图所示,分两种情况考虑:
当D1为OC中点时,△D1OB的面积是△COB的一半,此时D1(
| 3 |
| 2 |
| 3 |
| 2 |
当O为D1D2中点时,△DOB的面积是△COB的一半,此时D2(-
| 3 |
| 2 |
| 3 |
| 2 |
综上,D的坐标为(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(4)分两种情况考虑:
当直线a在C左侧时,此时EF=-x+6-x≤3,
解得:x≥
| 3 |
| 2 |
当直线a在C右侧时,此时EF=x-(-x+6)≤3,
解得:x≤
| 9 |
| 2 |
则x的范围为
| 3 |
| 2 |
| 9 |
| 2 |
点评:此题属于一次函数综合题,涉及的知识有:两条直线的交点坐标,坐标与图形性质,勾股定理,以及勾股定理的逆定理,线段中点坐标公式,利用了数形结合及分类讨论的思想,弄清题意是解本题的关键.

练习册系列答案
相关题目
 如图,已知AP平分∠BAC,DP平分∠CDB,∠C=50°,∠B=20°,则∠P的度数为( )
如图,已知AP平分∠BAC,DP平分∠CDB,∠C=50°,∠B=20°,则∠P的度数为( )| A、10° | B、15° |
| C、30° | D、40° |
使分式
有意义的x的取值范围是( )
| 2 |
| x-3 |
| A、x≤3 | B、x≥3 |
| C、x≠3 | D、x=3 |
估计
的值在( )之间.
| 11 |
| A、1和2 | B、2和3 |
| C、3和4 | D、4与5 |
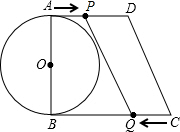 如图,AB是圆O的直径,AD、BC都垂直于AB,AD=13cm,BC=16cm,DC=5cm,点P、Q是动点,点P以1cm/s的速度由A向D运动,同时Q从C向B以2cm/s的速度运动,当其中一点到达时,另一点同时停止运动.
如图,AB是圆O的直径,AD、BC都垂直于AB,AD=13cm,BC=16cm,DC=5cm,点P、Q是动点,点P以1cm/s的速度由A向D运动,同时Q从C向B以2cm/s的速度运动,当其中一点到达时,另一点同时停止运动. 已知:如图,在△ABC中,AB=AC,过点A作MN∥BC,点D、E在直线MN上,且DA=EA≠
已知:如图,在△ABC中,AB=AC,过点A作MN∥BC,点D、E在直线MN上,且DA=EA≠
 如图,在正方形网格中,每个小正方形的边长都是1个单位长度,△ABC和△DEF的三个顶点都在格点上.
如图,在正方形网格中,每个小正方形的边长都是1个单位长度,△ABC和△DEF的三个顶点都在格点上.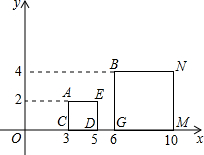 如图,在直角坐标系中,点A、B的坐标分别为(3,2)、(6,4),AC⊥x轴于点C,BG⊥x轴于点G,分别以AC、BG为边作正方形ACDE和正方形BGMN;
如图,在直角坐标系中,点A、B的坐标分别为(3,2)、(6,4),AC⊥x轴于点C,BG⊥x轴于点G,分别以AC、BG为边作正方形ACDE和正方形BGMN;