题目内容
14. 如图,已知直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E,求证:DE是⊙O的切线.
如图,已知直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E,求证:DE是⊙O的切线.
分析 连结OD,如图,由AD平分∠CAM得∠1=∠2,加上∠2=∠3,则∠1=∠3,于是可判断OD∥MN,由于DE⊥MN,所以OD⊥DE,则可根据切线的判定定理得到DE是⊙O的切线.
解答 证明: 连结OD,如图,
连结OD,如图,
∵AD平分∠CAM,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠3,
∴∠1=∠3,
∴OD∥MN,
∵DE⊥MN,
∴OD⊥DE,
∴DE是⊙O的切线.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列运算正确的是( )
| A. | 2a2+3a3=5a5 | B. | (a2)4=a6 | C. | a4÷a=a3 | D. | (x+y)2=x2+y2 |
19. 已知点A(-2,y1)和点B(1,y2)是如图所示的一次函数y=2x+b图象上的两点,则y1与y2的大小关系是( )
已知点A(-2,y1)和点B(1,y2)是如图所示的一次函数y=2x+b图象上的两点,则y1与y2的大小关系是( )
 已知点A(-2,y1)和点B(1,y2)是如图所示的一次函数y=2x+b图象上的两点,则y1与y2的大小关系是( )
已知点A(-2,y1)和点B(1,y2)是如图所示的一次函数y=2x+b图象上的两点,则y1与y2的大小关系是( )| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | y1≥y2 |
 如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=50度.
如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=50度. 如图,已知,A(0,4),B(-3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=$\frac{k}{x}$的图象经过D点.
如图,已知,A(0,4),B(-3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=$\frac{k}{x}$的图象经过D点. 如图,在△ABC中,AB=AC,点D在边BC上,连接AD,将线段AD绕点A逆时针旋转到AE,使得∠DAE=∠BAC,连接DE交AC于F,请写出图中一对相似的三角形:△ABD∽AEF(只要写出一对即可).
如图,在△ABC中,AB=AC,点D在边BC上,连接AD,将线段AD绕点A逆时针旋转到AE,使得∠DAE=∠BAC,连接DE交AC于F,请写出图中一对相似的三角形:△ABD∽AEF(只要写出一对即可).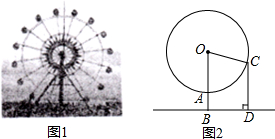 图1是某游乐场的摩天轮,图2是它的正面示意图,已知摩天轮的半径为40米,每分钟绕圆心O匀速旋转15°,其最低点A离地面的距离AB为5米,小明从点A处登上摩天轮,5分钟后旋转到点C,此时小明绕点O旋转了多少度?他离地面的高度CD是多少米?(结果精确到0.1米)
图1是某游乐场的摩天轮,图2是它的正面示意图,已知摩天轮的半径为40米,每分钟绕圆心O匀速旋转15°,其最低点A离地面的距离AB为5米,小明从点A处登上摩天轮,5分钟后旋转到点C,此时小明绕点O旋转了多少度?他离地面的高度CD是多少米?(结果精确到0.1米)