题目内容
4.(1)求不等式组$\left\{\begin{array}{l}{2x+2≥0}\\{3x-5<0}\end{array}\right.$的整数解;(2)化简:(1+$\frac{1}{x-1}$)÷$\frac{x}{{x}^{2}-1}$.
分析 (1)分别求出各不等式的解集,再求出其公共解集,并得出x的整数解即可;
(2)根据分式混合运算的法则进行逐一计算即可.
解答 解:(1)$\left\{\begin{array}{l}2x+2≥0①\\ 3x-5<0②\end{array}\right.$,
由①得,x≥-1,
由②得,x<$\frac{5}{3}$,
故不等式组的解集为:-1≤x<$\frac{5}{3}$,其整数解为-1,0,1;
(2)原式=$\frac{x}{x-1}$•$\frac{(x+1)(x-1)}{x}$
=x+1.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
13.顺次连接下面四边形各边中点,得到的四边形一定是正方形的是( )
| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |
 如图,已知直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E,求证:DE是⊙O的切线.
如图,已知直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E,求证:DE是⊙O的切线. 如图,在△ABC中,AB=6cm,AC=4cm,BC的垂直平分线分别角AB、BC于D、E,则△ACD的周长为10cm.
如图,在△ABC中,AB=6cm,AC=4cm,BC的垂直平分线分别角AB、BC于D、E,则△ACD的周长为10cm.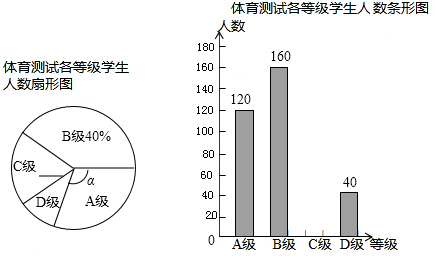
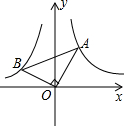 如图,已知第一象限内的点A在反比例函数y=$\frac{1}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{1}{3}$.
如图,已知第一象限内的点A在反比例函数y=$\frac{1}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{1}{3}$.