题目内容
14. 如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=50度.
如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=50度.
分析 由在⊙O中,AB为直径,根据直径所对的圆周角是直角,可求得∠ADB=90°,又由圆周角定理,可求得∠B=∠ACD=40°,继而求得答案.
解答 解:∵在⊙O中,AB为直径,
∴∠ADB=90°,
∵∠B=∠ACD=40°,
∴∠BAD=90°-∠B=50°.
故答案为:50.
点评 此题考查了圆周角定理.注意在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;半圆(或直径)所对的圆周角是直角.

练习册系列答案
相关题目
4. 如图,AB∥CD,∠A=50°,则∠1的大小是( )
如图,AB∥CD,∠A=50°,则∠1的大小是( )
 如图,AB∥CD,∠A=50°,则∠1的大小是( )
如图,AB∥CD,∠A=50°,则∠1的大小是( )| A. | 50° | B. | 120° | C. | 130° | D. | 150° |
2.下列运算正确的是( )
| A. | a6÷a3=a2 | B. | 5a2-3a2=2a | C. | (a3)3=a9 | D. | (a-b)2=a2-b2 |
3. 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )
 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )| A. | 圆柱 | B. | 圆锥 | C. | 长方体 | D. | 正方体 |
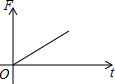
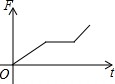
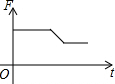
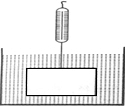 如图,挂在弹簧称上的长方体铁块浸没在水中,提着弹簧称匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧称的读数F(kg)与时间t(s)的函数图象大致是( )
如图,挂在弹簧称上的长方体铁块浸没在水中,提着弹簧称匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧称的读数F(kg)与时间t(s)的函数图象大致是( )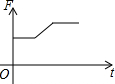
 如图,已知直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E,求证:DE是⊙O的切线.
如图,已知直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E,求证:DE是⊙O的切线.