题目内容
6.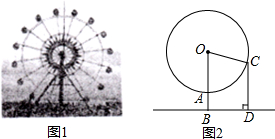 图1是某游乐场的摩天轮,图2是它的正面示意图,已知摩天轮的半径为40米,每分钟绕圆心O匀速旋转15°,其最低点A离地面的距离AB为5米,小明从点A处登上摩天轮,5分钟后旋转到点C,此时小明绕点O旋转了多少度?他离地面的高度CD是多少米?(结果精确到0.1米)
图1是某游乐场的摩天轮,图2是它的正面示意图,已知摩天轮的半径为40米,每分钟绕圆心O匀速旋转15°,其最低点A离地面的距离AB为5米,小明从点A处登上摩天轮,5分钟后旋转到点C,此时小明绕点O旋转了多少度?他离地面的高度CD是多少米?(结果精确到0.1米)
分析 由“旋转的角度=速度×时间”来计算得到小明绕点O旋转了75度.如图,过点C作CE⊥OB于点E,构建矩形BDCE和直角△OEC,利用矩形的性质和解该直角三角形来求CD的长度即可.
解答 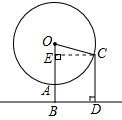 解:∵15×5°=75°,
解:∵15×5°=75°,
∴小明绕点O旋转了75度.
如图,过点C作CE⊥OB于点E,则四边形BDCE是矩形,
∴CD=BE.
由题意可知,∠AOC=75°,OC=40米,OB=45米.
在直角△OEC中,∵cos∠COE=$\frac{OE}{OC}$,
∴OE=OC•cos∠COE=40cos75°,
∴CD=EB=OB-OE=45-40cos75°≈34.6(米).
答:此时小明绕点O旋转了75度,他离地面的高度CD约为34.6米.
点评 本题考查了解直角三角形的应用.主要是余弦概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
相关题目
18.在平面直角坐标系中,点M(-2,1)关于x轴对称的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,已知直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E,求证:DE是⊙O的切线.
如图,已知直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E,求证:DE是⊙O的切线. 如图,四边形ABCD是⊙O的内接四边形,若∠A=75°,则∠C=105°.
如图,四边形ABCD是⊙O的内接四边形,若∠A=75°,则∠C=105°. 如图,在△ABC中,AB=6cm,AC=4cm,BC的垂直平分线分别角AB、BC于D、E,则△ACD的周长为10cm.
如图,在△ABC中,AB=6cm,AC=4cm,BC的垂直平分线分别角AB、BC于D、E,则△ACD的周长为10cm.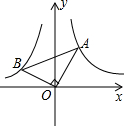 如图,已知第一象限内的点A在反比例函数y=$\frac{1}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{1}{3}$.
如图,已知第一象限内的点A在反比例函数y=$\frac{1}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{1}{3}$.