题目内容
11.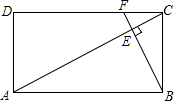 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}$=$\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{1}{16}$.
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}$=$\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{1}{16}$.
分析 首先根据$\frac{AD}{AB}$=$\frac{1}{2}$设AD=BC=a,则AB=CD=2a,然后利用勾股定理得到AC=$\sqrt{5}$a,然后根据射影定理得到BC2=CE•CA,AB2=AE•AC从而求得CE=$\frac{\sqrt{5}a}{5}$,AE=$\frac{4\sqrt{5}a}{5}$,得到$\frac{CE}{AE}$=$\frac{1}{4}$,利用△CEF∽△AEB,求得$\frac{{S}_{1}}{{S}_{2}}$=($\frac{CE}{AE}$)2=$\frac{1}{16}$.
解答 解:∵$\frac{AD}{AB}$=$\frac{1}{2}$,
∴设AD=BC=a,则AB=CD=2a,
∴AC=$\sqrt{5}$a,
∵BF⊥AC,
∴△CBE∽△CAB,△AEB∽△ABC,
∴BC2=CE•CA,AB2=AE•AC
∴a2=CE•$\sqrt{5}$a,2a2=AE•$\sqrt{5}$a,
∴CE=$\frac{\sqrt{5}a}{5}$,AE=$\frac{4\sqrt{5}a}{5}$,
∴$\frac{CE}{AE}$=$\frac{1}{4}$,
∵△CEF∽△AEB,
∴$\frac{{S}_{1}}{{S}_{2}}$=($\frac{CE}{AE}$)2=$\frac{1}{16}$,
故答案为:$\frac{1}{16}$.
点评 本题考查了矩形的性质及相似三角形的判定,能够牢记射影定理的内容对解决本题起到至关重要的作用,难度不大.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6.下面四个几何体中,俯视图是圆的几何体共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.4的平方根是( )
| A. | ±16 | B. | ±2 | C. | -2 | D. | 2 |
1.在实数$-\frac{2}{3}$,$\sqrt{7}$,0,-$\frac{π}{3}$中,最小的实数是( )
| A. | -$\frac{2}{3}$ | B. | $\sqrt{7}$ | C. | 0 | D. | -$\frac{π}{3}$ |
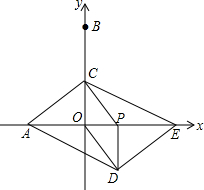 如图,在平面直角坐标系中,点A,B的坐标分别为(-3,0),(0,6).动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造平行四边形PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
如图,在平面直角坐标系中,点A,B的坐标分别为(-3,0),(0,6).动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造平行四边形PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.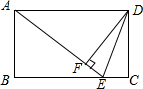 如图,在矩形ABCD中,E是BC上一点,且AE=BC,DF⊥AE,垂足是F,连接DE.求证:(1)DF=AB;(2)DE是∠FDC的平分线.
如图,在矩形ABCD中,E是BC上一点,且AE=BC,DF⊥AE,垂足是F,连接DE.求证:(1)DF=AB;(2)DE是∠FDC的平分线.