题目内容
3. 如图,P为正方形ABCD的AD边上一点,PE⊥AD交BD于点E点,将△PCD绕C点逆时针方向旋转90°到△FCB的位置,连接PF交BD于Q点.
如图,P为正方形ABCD的AD边上一点,PE⊥AD交BD于点E点,将△PCD绕C点逆时针方向旋转90°到△FCB的位置,连接PF交BD于Q点.①求证:BQ=EQ;
②探究线段PQ与线段CQ的关系,并证明你的结论.
分析 (1)先证明△PDE为等腰直角三角形,从而得到PD=PE,然后由PE=BF且PE∥BF,可得到四边形BFEP为平行四边形,最后依据平行四边形对角线的性质进行证明即可;
(2)由旋转的性质可得到△PCF为等腰直角三角形,依据直角三角形斜边上的中线的性质可得到PQ与CQ的数量关系,依据等腰三角形三线合一的性质可得到QC与PQ的位置关系.
解答 解:(1)∵ABCD为正方形,
∴∠PDE=45°.
∵PE⊥AD,
∴△PDE为等腰直角三角形.
∴PD=PE.
由旋转的性质可知PD=BF.
∴PE=BF.
∵BF⊥AD,PE⊥AD,
∴BF∥PE.
∴四边形BFPE为平行四边形.
∴BQ=EQ.
(2)QC⊥PQ且QC=PQ.
理由:∵四边形BFPE为平行四边形.
∴QF=QP.
由旋转的性质可知PC=CF,∠DCP=∠BCF.
∴∠DCB=∠PCF=90°.
∴△PCF为等腰直角三角形.
又∵PQ=FQ,
∴QC⊥PQ且QC=PQ.
点评 本题主要考查的是正方形的性质、平行四边形的性质和判定、旋转的性质、等腰直角三角形的性质,熟练掌握相关知识是解题的关键.

练习册系列答案
相关题目
13.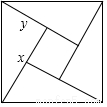 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x•y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x•y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x•y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x•y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )| A. | ①③ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
14.下列各组数能构成勾股数的是( )
| A. | 2,$\sqrt{3}$,$\sqrt{7}$ | B. | 12,16,20 | C. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | D. | 32,42,52 |
11.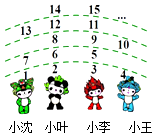 如图四个小朋友站成一排,老师按图中所示的规则数数,数到2016时对应的小朋友可得一朵红花.那么,得红花的小朋友是( )
如图四个小朋友站成一排,老师按图中所示的规则数数,数到2016时对应的小朋友可得一朵红花.那么,得红花的小朋友是( )
 如图四个小朋友站成一排,老师按图中所示的规则数数,数到2016时对应的小朋友可得一朵红花.那么,得红花的小朋友是( )
如图四个小朋友站成一排,老师按图中所示的规则数数,数到2016时对应的小朋友可得一朵红花.那么,得红花的小朋友是( )| A. | 小沈 | B. | 小叶 | C. | 小李 | D. | 小王 |
19.以下条件不可以判定△ABC与△A′B′C′相似的是( )
| A. | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{BC}{B′C′}$ | B. | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,且∠A=∠A’ | ||
| C. | ∠A=∠B’,∠B=∠C’ | D. | $\frac{AC}{A′C′}$=$\frac{BC}{B′C′}$,且∠A=∠A’ |
 解不等式15-9x<10-4x,并把解集在数轴上表示出来.
解不等式15-9x<10-4x,并把解集在数轴上表示出来.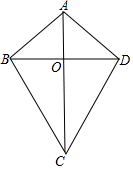 定义:有两组邻边相等的四边形是筝形
定义:有两组邻边相等的四边形是筝形