题目内容
9.二次函数y=x2-4的图象与x轴交于A,B两点,F为它的顶点,则S△ABF=8.分析 令y=0得x2-4=0可求得点BA的坐标,然后令x=0可求得y=-4,从而得到点F的坐标,然后利用三角形的面积公式求解即可.
解答 解:(1)当y=0时,x2-4=0,解得x1=-2,x2=2,
∴A(-2,0),B(2,0).
∴抛物线的对称轴为x=0.
将x=0代入得:y=-4.
∴抛物线顶点坐标为(0,-4),
所以△ABC的面积=$\frac{1}{2}$×(2+2)×4=8.
故答案为:8.
点评 本题主要考查的是抛物线与x轴的交点问题,将函数问题转化为方程问题是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
17.方程x(x+2)=3(x+2)的解是( )
| A. | 3和-2 | B. | 3 | C. | -2 | D. | 无解 |
 如图,将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN,EF交AD于点P.若△PDE的周长为18,且AM=2,求线段EC的长.
如图,将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN,EF交AD于点P.若△PDE的周长为18,且AM=2,求线段EC的长.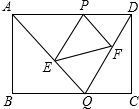 如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A,D),Q是BC边上的任意一点,连接AQ,DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A,D),Q是BC边上的任意一点,连接AQ,DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
 如图,电信部门要在S区修建一座发射塔.按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应建在什么位置?在图上标出它的位置.(尺规作图)
如图,电信部门要在S区修建一座发射塔.按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应建在什么位置?在图上标出它的位置.(尺规作图)