题目内容
1.已知,在△ABC中,∠BAC=90°,D,E,F在BC上,且BD=DE=EF=FC.(1)如果AB=AC,求证:tan∠BAD•tan∠CAF=$\frac{1}{9}$;
(2)如果AB≠AC,则上题中结论是否仍成立?如成立,请证明;如不成立,请说明理由.

分析 (1)设BD=x,则BC=4x,根据等腰直角三角形的性质得到DH=BH=$\frac{\sqrt{2}}{2}$x,AB=2$\sqrt{2}$x,求得tan∠BAD=$\frac{DH}{AH}$=$\frac{\frac{\sqrt{2}}{2}x}{\frac{3\sqrt{2}}{2}x}$=$\frac{1}{3}$,同理tan∠CAF=$\frac{1}{3}$,于是得到结论;
(2)过D作DH⊥AB于H,过F作FG⊥AC于G,得到FG∥AB,DH∥AC,推出△BDH≌△CFG,由全等三角形的性质得到DH=CG,BH=FG,通过△BDH∽△ABC,△CFG∽△ABC,得到$\frac{BD}{BC}$=$\frac{DH}{AC}=\frac{BH}{AB}$=$\frac{1}{4}$,$\frac{CF}{BC}$=$\frac{GF}{AB}=\frac{CG}{AC}$=$\frac{1}{4}$,于是得到$\frac{CG}{AG}=\frac{BH}{AH}$=$\frac{1}{3}$,等量代换得到$\frac{DH}{AG}=\frac{GF}{AH}$=$\frac{1}{3}$即可得到结论.
解答  证明:(1)设BD=x,则BC=4x,
证明:(1)设BD=x,则BC=4x,
如图1,过D作DH⊥AB于H,
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
∴DH=BH=$\frac{\sqrt{2}}{2}$x,AB=2$\sqrt{2}$x,
∴AH=AB-BH=$\frac{3\sqrt{2}}{2}$x,
∴tan∠BAD=$\frac{DH}{AH}$=$\frac{\frac{\sqrt{2}}{2}x}{\frac{3\sqrt{2}}{2}x}$=$\frac{1}{3}$,
同理tan∠CAF=$\frac{1}{3}$,
∴tan∠BAD•tan∠CAF=$\frac{1}{9}$;
(2)成立, 如图2,过D作DH⊥AB于H,过F作FG⊥AC于G,
如图2,过D作DH⊥AB于H,过F作FG⊥AC于G,
∴FG∥AB,DH∥AC,
∴∠GFC=∠B,
在△BDH与△CFG中,
$\left\{\begin{array}{l}{∠BHD=∠CGF}\\{∠B=∠GFC}\\{BD=CF}\end{array}\right.$,
∴△BDH≌△CFG,
∴DH=CG,BH=FG,
∵FG∥AB,DH∥AC,
∴△BDH∽△ABC,△CFG∽△ABC,
∴$\frac{BD}{BC}$=$\frac{DH}{AC}=\frac{BH}{AB}$=$\frac{1}{4}$,$\frac{CF}{BC}$=$\frac{GF}{AB}=\frac{CG}{AC}$=$\frac{1}{4}$,
∴$\frac{CG}{AC}=\frac{BH}{AB}$=$\frac{1}{4}$,
∴$\frac{CG}{AG}=\frac{BH}{AH}$=$\frac{1}{3}$,
∴$\frac{DH}{AG}=\frac{GF}{AH}$=$\frac{1}{3}$
∴tan∠BAD•tan∠CAF=$\frac{DH}{AH}•\frac{GF}{AG}$=$\frac{DH}{AG}=\frac{FG}{AH}$=$\frac{1}{9}$.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,等腰直角三角形的性质,三角函数,熟练掌握相似三角形的判定和性质是解题的关键.

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
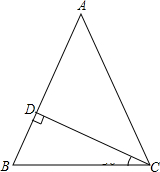 已知:如图,△ABC中,AB=AC,CD⊥AB于点D.求证:∠BAC=2∠DCB.(温馨提示:要用到三线合一的性质哟!聪明的你想到了吗?)
已知:如图,△ABC中,AB=AC,CD⊥AB于点D.求证:∠BAC=2∠DCB.(温馨提示:要用到三线合一的性质哟!聪明的你想到了吗?) 已知:如图,有一块锐角三角形余料ABC,它的边BC=12cm,高AH=8cm,要把它加工成矩形零件,使矩形零件的一边DE在BC边上,其余两个顶点G、F分别在边AB和AC上.
已知:如图,有一块锐角三角形余料ABC,它的边BC=12cm,高AH=8cm,要把它加工成矩形零件,使矩形零件的一边DE在BC边上,其余两个顶点G、F分别在边AB和AC上.