题目内容
求下列函数的开口方向、对称轴及顶点坐标.
(1)y=-0.5(x+1)2;
(2)y=2(x-2)2+5;
(3)y=-
(x-3)2.
(1)y=-0.5(x+1)2;
(2)y=2(x-2)2+5;
(3)y=-
| 3 |
| 4 |
考点:二次函数的性质
专题:
分析:分别根据二次函数的性质确定抛物线开口方向、对称轴和顶点坐标.
解答:解:(1)抛物线开口向下,对称轴为直线x=-1,顶点坐标为(-1,0);
(2)抛物线开口向上,对称轴为直线x=2,顶点坐标为(2,5);
(3)抛物线开口向下,对称轴为直线x=3,顶点坐标为(3,0).
(2)抛物线开口向上,对称轴为直线x=2,顶点坐标为(2,5);
(3)抛物线开口向下,对称轴为直线x=3,顶点坐标为(3,0).
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.
当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
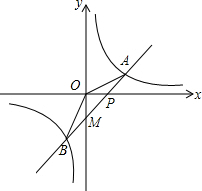 如图,一次函数y=kx-1的图象和反比例函数y=
如图,一次函数y=kx-1的图象和反比例函数y= 图②是由图①中的△ABC沿DE折叠得到的,如果∠A=30°,猜想∠BDA,∠CEA,∠A之间的数量关系为
图②是由图①中的△ABC沿DE折叠得到的,如果∠A=30°,猜想∠BDA,∠CEA,∠A之间的数量关系为