题目内容
 图②是由图①中的△ABC沿DE折叠得到的,如果∠A=30°,猜想∠BDA,∠CEA,∠A之间的数量关系为
图②是由图①中的△ABC沿DE折叠得到的,如果∠A=30°,猜想∠BDA,∠CEA,∠A之间的数量关系为考点:三角形内角和定理,翻折变换(折叠问题)
专题:
分析:如图,首先证明∠B+∠C+∠BDE+∠CED=360°①;由图①证明∠B+∠C=180°-∠A,由图②∠BDE+∠CED=x°+y°+(180°-∠A),代入①式整理,问题即可解决.
解答: 解:猜想:∠BDA+∠CEA=2∠A.
解:猜想:∠BDA+∠CEA=2∠A.
在图2中,∵∠B+∠C+∠BDE+∠CED=360°,
而∠BDE+∠CED=x°+y°+(180°-∠A),
∠B+∠C=180°-∠A,
∴x°+y°+360°-2∠A=360°,
∴x°+y°=2∠A,
故该题答案为:∠BDA+∠CEA=2∠A.
 解:猜想:∠BDA+∠CEA=2∠A.
解:猜想:∠BDA+∠CEA=2∠A.在图2中,∵∠B+∠C+∠BDE+∠CED=360°,
而∠BDE+∠CED=x°+y°+(180°-∠A),
∠B+∠C=180°-∠A,
∴x°+y°+360°-2∠A=360°,
∴x°+y°=2∠A,
故该题答案为:∠BDA+∠CEA=2∠A.
点评:该题主要考查了翻折变换、三角形的内角和定理及其应用问题;解题的关键是灵活运用有关定理来分析、解答.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图是一个表面带有图案的正方体,则其表面展开图可能是( )
如图是一个表面带有图案的正方体,则其表面展开图可能是( )A、 |
B、 |
C、 |
D、 |
 已知,△ABC内接于⊙O,AB=BC,∠BAC平分线交于⊙O于点P,自P点作PD⊥AB,垂足为D,求证:AB-AC=2BD.
已知,△ABC内接于⊙O,AB=BC,∠BAC平分线交于⊙O于点P,自P点作PD⊥AB,垂足为D,求证:AB-AC=2BD. 如图为二次函数y=ax2+bx+c的图象,在下列说法中:
如图为二次函数y=ax2+bx+c的图象,在下列说法中: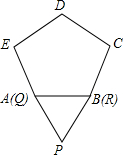 如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为
如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为 如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上. 在正方形方格中,△ABC的顶点A、B、C在单位正方形的顶点上,请在图中画一个格点△A1B1C1使△A1B1C1∽△ABC(相似比不为1),且点都在单位正方形的顶点上.
在正方形方格中,△ABC的顶点A、B、C在单位正方形的顶点上,请在图中画一个格点△A1B1C1使△A1B1C1∽△ABC(相似比不为1),且点都在单位正方形的顶点上.